题目内容
19.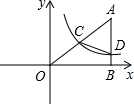 如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D.
如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D.(1)求反比例函数解析式;
(2)若函数y=3x与y=$\frac{k}{x}$的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
分析 (1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=$\frac{k}{x}$中,即可确定反比例函数解析式;
(2)先将y=3x与y=$\frac{12}{x}$联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
解答 解:(1)∵A点的坐标为(8,y),
∴OB=8,
∵AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,
∴$\frac{OB}{OA}=\frac{4}{5}$,
∴OA=10,
由勾股定理得:AB=$\sqrt{O{A}^{2}-O{B}^{2}}=6$,
∵点C是OA的中点,且在第一象限内,
∴C(4,3),
∵点C在反比例函数y=$\frac{k}{x}$的图象上,
∴k=12,
∴反比例函数解析式为:y=$\frac{12}{x}$;
(2)将y=3x与y=$\frac{12}{x}$联立成方程组,得:
$\left\{\begin{array}{l}{y=3x}\\{y=\frac{12}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=6}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-6}\end{array}\right.$,
∵M是直线与双曲线另一支的交点,
∴M(-2,-6),
∵点D在AB上,
∴点D的横坐标为8,
∵点D在反比例函数y=$\frac{12}{x}$的图象上,
∴点D的纵坐标为$\frac{3}{2}$,
∴D(8,$\frac{3}{2}$),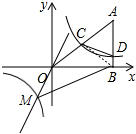
∴BD=$\frac{3}{2}$,
连接BC,如图所示,
∵S△MOB=$\frac{1}{2}$•8•|-6|=24,
S四边形OCDB=S△OBC+S△BCD=$\frac{1}{2}$•8•3+$\frac{1}{2}•\frac{3}{2}•4$=15,
∴$\frac{S△MOB}{S四边形OCDB}=\frac{24}{15}=\frac{8}{5}$.
点评 本题考查了一次函数与反比例函数的交点问题,用待定系数法求反比例函数的解析式及计算图形面积的问题.解题的关键是:确定交点的坐标.

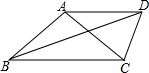 如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
①垂直于弦的直径平分线以及弦所对的两条弧.②平分弦的直径垂直于这条弦,并且平分这条弦所对的两条弧.③弦的垂直平分线经过圆心,并且平分这条弦所对的两条弦.④平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

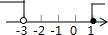


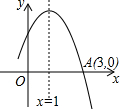 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( ) 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: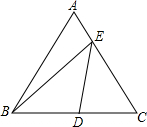 如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.
如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.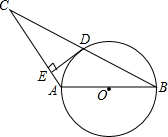 如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.