题目内容
4.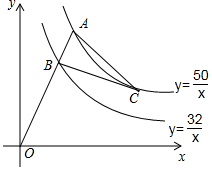 如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{3}}{13}$ |
分析 根据勾股定理得到BO=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,B(4,8),得到S△BOD=16,求得S△AOE=25根据相似三角形的性质得到AO=5$\sqrt{5}$,得到AB=$\sqrt{5}$根据相似三角形的性质得到OE=5,AE=10,求得A(5,10)待定系数法得到直线OA的解析式为:y=2x,设直线BC的解析式为y=-$\frac{1}{2}$x+b,求得直线BC的解析式为y=-$\frac{1}{2}$x+10,解方程组得到C(10,5),于是得到结论.
解答 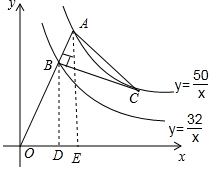 解:把x=4代入y=$\frac{32}{x}$得,y=8,
解:把x=4代入y=$\frac{32}{x}$得,y=8,
∴BO=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,B(4,8),
∴S△BOD=16,
∵S△AOE=25,
∵△OBD∽△OAE,
∴$\frac{{S}_{△BOD}}{{S}_{△AOE}}$=($\frac{BO}{AO}$)2,
∴($\frac{4\sqrt{5}}{OA}$)2=$\frac{16}{25}$,
∴AO=5$\sqrt{5}$,
∴AB=$\sqrt{5}$,
∵△OBD∽△OAE,
∴$\frac{OD}{OE}=\frac{BD}{AE}=\frac{OB}{OA}$=$\frac{4\sqrt{5}}{5\sqrt{5}}$,
∴OE=5,AE=10,
∴A(5,10)
∵直线OA的解析式为:y=2x,
∵BC⊥OA,
∴设直线BC的解析式为y=-$\frac{1}{2}$x+b,
∴8=-$\frac{1}{2}×4$+b,
∴b=10,
∴直线BC的解析式为y=-$\frac{1}{2}$x+10,
解$\left\{\begin{array}{l}{y=\frac{50}{x}}\\{y=-\frac{1}{2}x+10}\end{array}\right.$得$\left\{\begin{array}{l}{x=10}\\{y=5}\end{array}\right.$,
∴C(10,5),
∴AC=$\sqrt{(10-5)^{2}+(5-10)^{2}}$=5$\sqrt{2}$,
∴cos∠BAC=$\frac{AB}{AC}$=$\frac{\sqrt{5}}{5\sqrt{2}}$=$\frac{\sqrt{10}}{10}$,
故选A.
点评 本题考查了反比例函数图象上点的坐标特征,解直角三角形,待定系数法求函数的解析式,正确的作出辅助线是解题的关键.

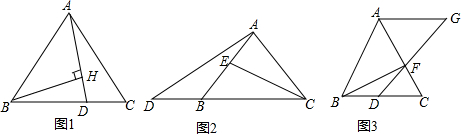
 如图,在正方形ABCD内,∠AFB=∠CED=90°,AF=CE,连结EF,若EF=3$\sqrt{2}$,两块阴影部分的面积和为4,则正方形ABCD的面积为( )
如图,在正方形ABCD内,∠AFB=∠CED=90°,AF=CE,连结EF,若EF=3$\sqrt{2}$,两块阴影部分的面积和为4,则正方形ABCD的面积为( )| A. | 17 | B. | 18 | C. | 26 | D. | 32 |
| A. | ①对,②错 | B. | ①错,②对 | C. | ①②都错 | D. | ①②都对 |
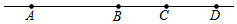 如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.
如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.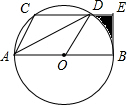 如图所示,CD是⊙O的弦,AB是⊙O的直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E.
如图所示,CD是⊙O的弦,AB是⊙O的直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E. (1)式子y=$\frac{\sqrt{x-2}}{x-3}$中自变量x的取值范围是x≥2且x≠3;
(1)式子y=$\frac{\sqrt{x-2}}{x-3}$中自变量x的取值范围是x≥2且x≠3;