题目内容
14.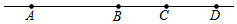 如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.
如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.
分析 根据线段的定义,中点的定义以及两点间的距离进行判断即可得出结论.
解答 解:由题可得,图中共有6条线段:AB,AC,AD,BC,BD,故①正确;
若B为AD的中点,C为BD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$,故②错误;
若一点M在B、C(包含B,C)之间,则点M到A、B、C、D四个点的距离之和为:AM+DM+CM+BM=AD+BC;
当点M在AB之间或CD之间时,点M到A、B、C、D四个点的距离之和大于AD+BC;故③正确;
故答案为:①③
点评 本题主要考查了两点间的距离以及线段的概念,解题时注意:线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA),连接两点间的线段的长度叫两点间的距离.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.一个三角形的三边长分别为4,7,x,那么x可能的值是( )
| A. | 3 | B. | 7 | C. | 11 | D. | 15 |
9. 如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
 如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )| A. | 带①去 | B. | 带②去 | C. | 带③去 | D. | 带①和②去 |
3. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.则C13的顶点坐标为( )
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.则C13的顶点坐标为( )
| A. | ($\frac{69}{2}$,$\frac{9}{4}$) | B. | ($\frac{69}{2}$,-$\frac{9}{4}$) | C. | ($\frac{75}{2}$,$\frac{9}{4}$) | D. | ($\frac{75}{2}$,-$\frac{9}{4}$) |
4.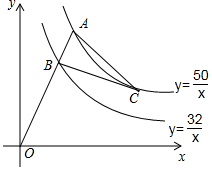 如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
 如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{3}}{13}$ |
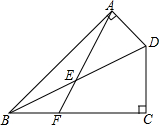 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.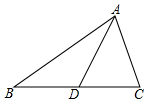 如图,△ABC中,AD是中线,AC=3,AB=5,则AD的取值范围是1<AD<4.
如图,△ABC中,AD是中线,AC=3,AB=5,则AD的取值范围是1<AD<4.