题目内容
10.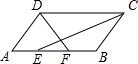 如图,平行四边形ABCD中,CE、DF分别是∠BCD、∠ADC的平分线,交AB于E、F,且AB=15,AD=8,则EF=1.
如图,平行四边形ABCD中,CE、DF分别是∠BCD、∠ADC的平分线,交AB于E、F,且AB=15,AD=8,则EF=1.
分析 由平行四边形ABCD中,CE、DF分别是∠BCD、∠ADC的平分线,易得△ADF与△BCE是等腰三角形,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴BC=AD=8,AB∥CD,
∴∠CDF=∠AFD,∠BEC=∠DCE,
∵CE、DF分别是∠BCD、∠ADC的平分线,
∴∠ADF=∠CDF,∠BCE=∠DCE,
∴∠ADF=∠AFD,∠BCE=∠BEC,
∴AF=AD=8,BE=BC=8,
∴EF=AF+BE-AB=8+8-15=1.
故答案为:1.
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△ADF与△BCE是等腰三角形是关键.

练习册系列答案
相关题目
1.已知a>1,点A(a-1,y1),B(a,y2),C(a+1,y3)都在二次函数y=-$\frac{1}{2}$x2的图象上,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分: 数a,b,c在数轴上的位置如图所示,化简|a-c|+|b-c|+|a+b|.
数a,b,c在数轴上的位置如图所示,化简|a-c|+|b-c|+|a+b|.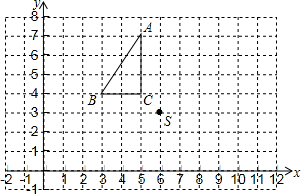 △ABC和点S在平面直角坐标系中的位置如图所示.
△ABC和点S在平面直角坐标系中的位置如图所示. 如图,梯形ABCD中,AD∥BC,∠DAE=∠C,AD=5,若此梯形的周长是29,则△ABE的周长是19.
如图,梯形ABCD中,AD∥BC,∠DAE=∠C,AD=5,若此梯形的周长是29,则△ABE的周长是19.