题目内容
1.已知a>1,点A(a-1,y1),B(a,y2),C(a+1,y3)都在二次函数y=-$\frac{1}{2}$x2的图象上,则( )| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
分析 先根据二次函数的性质得到抛物线的对称轴为y轴,然后比较三个点与y轴的远近得到y1、y2、y3的大小关系.
解答 解:∵二次函数的解析式为y=-$\frac{1}{2}$x2,
∴抛物线的对称轴为y轴,
∵A(a-1,y1),B(a,y2),C(a+1,y3),
∵a>1,
∴点A离y轴最近,点C离y轴最远,
而抛物线开口向下,
∴y3<y2<y1.
故选:C.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
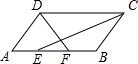 如图,平行四边形ABCD中,CE、DF分别是∠BCD、∠ADC的平分线,交AB于E、F,且AB=15,AD=8,则EF=1.
如图,平行四边形ABCD中,CE、DF分别是∠BCD、∠ADC的平分线,交AB于E、F,且AB=15,AD=8,则EF=1. 如图的正方体的平面展开图,如果将其折叠成正方体,那么图中的E,F两点分别与其他哪些点重合?
如图的正方体的平面展开图,如果将其折叠成正方体,那么图中的E,F两点分别与其他哪些点重合?