题目内容
5. 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:解:过点E作EF∥AB.
∴∠B=∠1.(两直线平行,内错角相等)
∵∠B=26°(已知),
∴∠1=26° (等量代换).
∵AB∥CD已知,
∵EF∥AB (作辅助线),
∴EF∥CD.
∴∠D=∠2.(两直线平行,内错角相等)
∵∠D=39° (已知),
∴∠2=39°(等量代换).
∴∠BED=65° (等式性质).
分析 作EF∥AB,如图,由于AB∥CD,则可判断AB∥EF∥CD,根据平行线的性质得∠1=∠B=26°,∠2=∠D=39°,于是得到∠BED=65°.
解答 解:过点E作EF∥AB.
∴∠B=∠1.(两直线平行,内错角相等)
∵∠B=26°(已知),
∴∠1=26° (等量代换).
∵AB∥CD已知,
∵EF∥AB (作辅助线),
∴EF∥CD.
∴∠D=∠2.(两直线平行,内错角相等)
∵∠D=39° (已知),
∴∠2=39°(等量代换).
∴∠BED=65° (等式性质).
故答案为:1,两直线平行,内错角相等,26,等量代换,已知,两直线平行,2,内错角相等,39,等量代换,65.
点评 本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了三角形外角性质.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
20.图中阴影部分的面积相等的是( )


| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | 无法判断 |
15. 张大伯计划建一个面积为72平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分用26米的竹篱笆围成,如图所示,如果设垂直于墙的一边长为x米,那么x满足的方程是( )
张大伯计划建一个面积为72平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分用26米的竹篱笆围成,如图所示,如果设垂直于墙的一边长为x米,那么x满足的方程是( )
 张大伯计划建一个面积为72平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分用26米的竹篱笆围成,如图所示,如果设垂直于墙的一边长为x米,那么x满足的方程是( )
张大伯计划建一个面积为72平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分用26米的竹篱笆围成,如图所示,如果设垂直于墙的一边长为x米,那么x满足的方程是( )| A. | x(13-x)=72 | B. | x(26-x)=72 | C. | x$\frac{(26-x)}{2}$=72 | D. | x(26-2x)=72 |
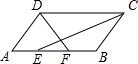 如图,平行四边形ABCD中,CE、DF分别是∠BCD、∠ADC的平分线,交AB于E、F,且AB=15,AD=8,则EF=1.
如图,平行四边形ABCD中,CE、DF分别是∠BCD、∠ADC的平分线,交AB于E、F,且AB=15,AD=8,则EF=1.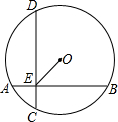 如图,⊙O的弦AB、CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2$\sqrt{10}$cm.求O到CD的距离,OE的长及⊙O的半径.
如图,⊙O的弦AB、CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2$\sqrt{10}$cm.求O到CD的距离,OE的长及⊙O的半径.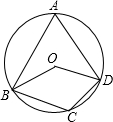 已知:如图,四边形ABCD内接于⊙O,∠BOD=120°,∠BAD=60°,∠BCD=120°.
已知:如图,四边形ABCD内接于⊙O,∠BOD=120°,∠BAD=60°,∠BCD=120°.