题目内容
 如图,四边形ABCD,DCFE,EFGH都是边长为1的正方形.
如图,四边形ABCD,DCFE,EFGH都是边长为1的正方形.(1)求证:△ACF∽△GCA;
(2)试说明∠1与∠2的和是一个定值.
考点:相似三角形的判定与性质
专题:
分析:(1)由对应边成比例及其夹角相等可得三角形相似;
(2)由(1)可得∠1=∠CAF,进而可得其和的大小.
(2)由(1)可得∠1=∠CAF,进而可得其和的大小.
解答: 解:(1)∵四边形ABCD,DCFE,EFGH都是边长为1的正方形,
解:(1)∵四边形ABCD,DCFE,EFGH都是边长为1的正方形,
∴CF=1,AC=
,CG=2,
∵
=
,
=
=
,
又∵∠ACF=∠GCA,
∴△ACF∽△GCA;
(2)由(1)得:△ACF∽△GCA,
∴∠1=∠GCA,
∴∠1+∠2=∠GAC+∠2=∠ACB=45°,
∴∠1与∠2的和是一个定值.
 解:(1)∵四边形ABCD,DCFE,EFGH都是边长为1的正方形,
解:(1)∵四边形ABCD,DCFE,EFGH都是边长为1的正方形,∴CF=1,AC=
| 2 |
∵
| AC |
| CG |
| ||
| 2 |
| CF |
| CA |
| 1 | ||
|
| ||
| 2 |
又∵∠ACF=∠GCA,
∴△ACF∽△GCA;
(2)由(1)得:△ACF∽△GCA,
∴∠1=∠GCA,
∴∠1+∠2=∠GAC+∠2=∠ACB=45°,
∴∠1与∠2的和是一个定值.
点评:本题主要考查了正方形的性质及相似三角形的判定及性质问题,应熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知平面内两点A(-1,-3),B(x,5),且AB=10,则x的值是( )
| A、5 | B、5或-5 |
| C、5或7 | D、5或-7 |
当x>2时,|1+
|等于( )
| (x-2)2 |
| A、1-x | B、x-1 |
| C、3-x | D、x-3 |
 如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).
如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).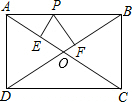 在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值.
在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值.