题目内容
在△ABC中，若AC=
，BC=
，AB=3，则∠A≈ ．
| 2 |
| 7 |
考点：解直角三角形
专题：
分析：由勾股定理的逆定理可判定△ABC为直角三角形，∠C=90°，再根据三角函数的定义可求得∠A的余弦，可求得∠A．
解答：解：∵在△ABC中，若AC=
，BC=
，AB=3，
∴AB2=AC2+BC2，
∴△ABC为直角三角形，∠C=90°，
∴cos∠A=
=
，
∴∠A≈62°，
故答案为：62°．
| 2 |
| 7 |
∴AB2=AC2+BC2，
∴△ABC为直角三角形，∠C=90°，
∴cos∠A=
| AC |
| AB |
| ||
| 3 |
∴∠A≈62°，
故答案为：62°．
点评：本题主要考查勾股定理的逆定理及三角函数的定义，利用勾股定理的逆定理判断出△ABC为直角三角形是解题的关键．
练习册系列答案
相关题目
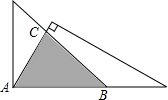一副三角板按如图所示位置摆放，测得BC=10cm，则两个三角板重叠（阴影）部分的面积为（ ）| A、75m2 | ||||
B、（25+25
| ||||
C、（25+
| ||||
D、（25+
|
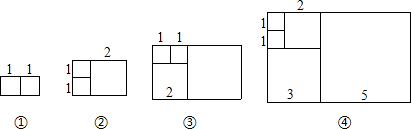
如图，四边形ABCD，DCFE，EFGH都是边长为1的正方形．