题目内容
 如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).
如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).考点:解直角三角形
专题:计算题
分析:作AH⊥BC于H,如图根据正弦的定义得到AH=ABsinB,再利用三角形面积公式得到∴△ABC的面积=
BC•AH=
•25•22•sin50°,然后进行近似数计算.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:作AH⊥BC于H,如图,
解:作AH⊥BC于H,如图,
在Rt△ABH中,∵sin∠B=
,
∴AH=ABsinB,
∴△ABC的面积=
BC•AH=
•25•22•sin50°≈72.1(cm2).
 解:作AH⊥BC于H,如图,
解:作AH⊥BC于H,如图,在Rt△ABH中,∵sin∠B=
| AH |
| AB |
∴AH=ABsinB,
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
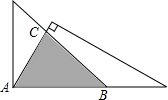 一副三角板按如图所示位置摆放,测得BC=10cm,则两个三角板重叠(阴影)部分的面积为( )
一副三角板按如图所示位置摆放,测得BC=10cm,则两个三角板重叠(阴影)部分的面积为( )| A、75m2 | ||||
B、(25+25
| ||||
C、(25+
| ||||
D、(25+
|
 如图,一次函数y=kx+3的图象与反比例函数y=
如图,一次函数y=kx+3的图象与反比例函数y= 如图,已知菱形ABCD,E、F是AB、BC的中点,求证:OE=OF.
如图,已知菱形ABCD,E、F是AB、BC的中点,求证:OE=OF. 如图,四边形ABCD,DCFE,EFGH都是边长为1的正方形.
如图,四边形ABCD,DCFE,EFGH都是边长为1的正方形.