题目内容
16.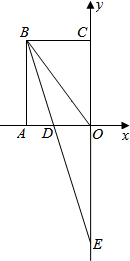 将矩形ABCO如图放置在平面直角坐标系中,∠ABO的平分线BE交x轴于点D,交y轴于点E,线段OA,OC(OA<OC)的长是一元二次方程x2-21x+108=0的两根,请你解答下列问题:
将矩形ABCO如图放置在平面直角坐标系中,∠ABO的平分线BE交x轴于点D,交y轴于点E,线段OA,OC(OA<OC)的长是一元二次方程x2-21x+108=0的两根,请你解答下列问题:(1)求点B的坐标;
(2)点F在线段OB上,若△ADF的面积为8,反比例函数y=$\frac{k}{x}$的图象经过点F,求k的值;
(3)在(2)的条件下,点P是直线BC上的点,在坐标平面内是否存在点Q,使点B,F,P,Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
分析 (1)求出已知方程的解得到OA与OC的长,即可确定出B的坐标;
(2)由四边形ABCO是矩形,得到四个角为直角,AB与CE平行,利用勾股定理求出BO的长,根据BE为角平分线,得到一对角相等,再由两直线平行内错角相等,等量代换及等角对等边得到BO=EO,根据AB与OE平行得到三角形ABD与三角形ODE相似,由相似得比例求出AD的长,根据三角形ADF面积求出F的纵坐标,过F作FM垂直于x轴,进而确定出三角形FOM与三角形BAO相似,由相似得比例求出OM的长,确定出F的坐标,即可求出k的值;
(3)如图所示,四边形Q1FBC,四边形Q2FCB,四边形A3BFC都为菱形,求出相应Q坐标即可.
解答  解:(1)方程x2-21x+108=0,
解:(1)方程x2-21x+108=0,
变形得:(x-9)(x-12)=0,
解得:x1=9,x2=12,
∵OA<OC,
∴OA=9,OC=12,
∴点B的坐标为(-9,12);
(2)∵四边形ABCO是矩形,
∴AB∥CE,∠BAO=90°,
在Rt△ABO中,根据勾股定理得:BO=$\sqrt{A{O}^{2}+A{B}^{2}}$=15,
∵BE平分∠ABO,
∴∠ABD=∠OBD,∠ABD=∠DEO,
∴∠ABD=∠OBD=∠DEO,
∴BO=OE=15,
∵△ABD∽△OED,
∴$\frac{AD}{9-AD}$=$\frac{AB}{OE}$=$\frac{12}{15}$=$\frac{4}{5}$,
∴AD=4,
∵S△ADF=8,点F在BO上,
∴$\frac{1}{2}$×4×yF=8,
∴yF=4,
过点F作FM⊥AO于点M,
∴FM∥AB,
∴△FMO∽△BAO,
∴$\frac{OM}{OA}$=$\frac{FM}{AB}$,即$\frac{OM}{9}$=$\frac{4}{12}$,
∴OM=3,
∴点F的坐标为(-3,4),
∴k=xy=-12;
(3)如图所示,满足题意得Q坐标分别为Q1(7,4);Q2(-13,4);Q3(-3,20).
点评 此题属于一次函数综合题,涉及的知识有:相似三角形的判定与性质,一元二次方程的解法,勾股定理,矩形的性质,坐标与图形性质,以及待定系数法求反比例函数解析式,熟练掌握相似三角形的判定与性质是解本题的关键.

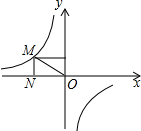 反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,则k的值为-6.
反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,则k的值为-6.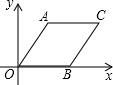 菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-3,1)或(3,-1).
菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-3,1)或(3,-1).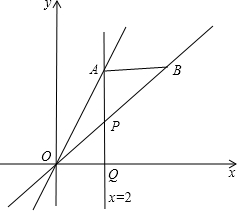 已知:直线y=2x与x=2相交于点A,直线x=2与x轴相交于点Q,点P是射线AQ上的一点,点B是直线OP上的一点,设AP=t,点B的坐标为(a,b).
已知:直线y=2x与x=2相交于点A,直线x=2与x轴相交于点Q,点P是射线AQ上的一点,点B是直线OP上的一点,设AP=t,点B的坐标为(a,b).