题目内容
6.某工厂现有甲种原材料380千克,乙种原材料290千克,计划用这两种原材料生产A、B两种产品共50件.已知生产一件A产品需要甲种原材料9千克,乙种原材料3千克,可获利700元;生产一件B产品需要甲种原材料4千克,乙种原材料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x.(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值,请指出此时原材料是否有结余.
分析 (1)根据等量关系:利润=A种产品的利润+B种产品的利润,可得出函数关系式;
(2)这是一道只有一个函数关系式的求最值问题,可根据等量关系:总利润=A种产品的利润+B种产品的利润,可得出函数关系式,然后根据函数的性质确定自变量的取值范围,由函数y随x的变化求出最大利润.
解答 解:(1)y=700x+1200(50-x),
即y=-500x+60000;
(2)由题意得:$\left\{\begin{array}{l}{9x+4(50-x)≤380}\\{3x+10(50-x)≤290}\end{array}\right.$
解得:30≤x≤36,
∵y=-500x+60000,k=-500<0,
∴y随x的增大而减小,
当x=30时,y最大=45000,
生产A种产品30件,B种产品20件,总利润y有最大值.y最大=45000元.
使用甲种原材料9×30+4×20=350(千克),结余30千克.
使用乙种原材料3×30+10×20=290(千克),恰好用尽.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
17.已知1米=109纳米,一个粒子的直径是35000纳米,用科学记数法表示直径为( )
| A. | 3.5×10-4米 | B. | 3.5×10-5米 | C. | 35×10-5米 | D. | 0.35×10-4米 |
1.钟表的时针与分针在运行过程中每隔一定时间就相遇一次,相遇间隔的时间是( )
| A. | 1小时 | B. | $\frac{12}{11}$小时 | C. | 1.2小时 | D. | 1.1小时 |
11.下列长度的三根木条,能组成三角形的是( )
| A. | 2,2,5 | B. | 2,2,4 | C. | 2,3,5 | D. | 2,3,4 |
15.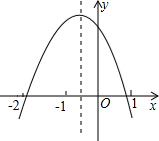 已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )| A. | abc>0 | B. | 2a-b<0 | C. | 4a-2b+c<0 | D. | (a+c)2>b2 |
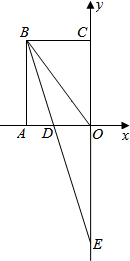 将矩形ABCO如图放置在平面直角坐标系中,∠ABO的平分线BE交x轴于点D,交y轴于点E,线段OA,OC(OA<OC)的长是一元二次方程x2-21x+108=0的两根,请你解答下列问题:
将矩形ABCO如图放置在平面直角坐标系中,∠ABO的平分线BE交x轴于点D,交y轴于点E,线段OA,OC(OA<OC)的长是一元二次方程x2-21x+108=0的两根,请你解答下列问题: