题目内容
11.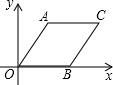 菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-3,1)或(3,-1).
菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-3,1)或(3,-1).
分析 根据菱形的对称性求出点B的坐标,再求出AB的中点的坐标,进而求出点C的坐标,根据向左平移横坐标减,向下平移纵坐标减求出平移后的C点对应的坐标,结合翻折变换知识求出沿x轴翻折后C点对应的坐标,再根据旋转的性质确定点P的坐标.
解答 解:∵菱形AOBC的点A坐标为(3,4),
∴点B的坐标为(5,0),
∴AB的中点的坐标为(4,2),
∴点C坐标为(8,4),
∵向左平移9个单位长度,再向下平移1个单位长度,
∴8-9=-1,4-1=3,
∴平移后点C对应的坐标为(-1,3),
沿x轴翻折后C点对应的坐标为(-1,-3),
∵在坐标平面内绕点O旋转90°,
∴若是顺时针旋转,则对应点在第二象限,坐标为(-3,1),
若是逆时针旋转,则对应点在第四象限,坐标为(3,-1),
综上所述,点P的坐标为(-3,1)或(3,-1),
故答案为(-3,1)或(3,-1).
点评 本题考查了菱形的性质,坐标与图形的变化,熟练掌握菱形的性质以及平移、旋转变换的性质是解题的关键.

练习册系列答案
相关题目
1.钟表的时针与分针在运行过程中每隔一定时间就相遇一次,相遇间隔的时间是( )
| A. | 1小时 | B. | $\frac{12}{11}$小时 | C. | 1.2小时 | D. | 1.1小时 |
2.一次函数y=kx+k(k<0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
19. 如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:
如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:
解答下列问题:
(1)表中的m=45,n=27.
(2)在扇形统计图中,“立定跳远”对应的圆心角的度数是72°.
(3)试估计全校1750名学生中参加“立定跳远”的人数.
 如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:
如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:| 项目名称 | 掷实心球 | 跳绳 | 50米短跑 | 立定跳远 | 仰卧起坐 | 健美操 |
| 人数 | 45 | 9 | m | 36 | n | 18 |
(1)表中的m=45,n=27.
(2)在扇形统计图中,“立定跳远”对应的圆心角的度数是72°.
(3)试估计全校1750名学生中参加“立定跳远”的人数.
6.腰长为10,一条中线长为6的等腰三角形的底边长为( )
| A. | 16 | B. | 8 | C. | 8或$\sqrt{22}$ | D. | 16或$\sqrt{22}$ |
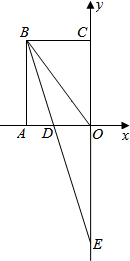 将矩形ABCO如图放置在平面直角坐标系中,∠ABO的平分线BE交x轴于点D,交y轴于点E,线段OA,OC(OA<OC)的长是一元二次方程x2-21x+108=0的两根,请你解答下列问题:
将矩形ABCO如图放置在平面直角坐标系中,∠ABO的平分线BE交x轴于点D,交y轴于点E,线段OA,OC(OA<OC)的长是一元二次方程x2-21x+108=0的两根,请你解答下列问题: