题目内容
15.某景区售出的门票分为成人票和儿童票,购买3张成人票和1张儿童票共需350元,购买1张成人票和2张儿童票共需200元.(1)求成人票和儿童票的单价;
(2)若干家庭结伴到该景区旅游,成人和儿童共30人.售票处规定:一次性购票数量达到30张,可购买团体票,每张票均按成人票价的八折出售,请你帮助他们选择花费最少的购票方式.
分析 (1)设每张成人票x元,每张儿童票y元,根据购买3张成人票和2张儿童票共需350元,购买1张成人票和2张儿童票共需200元,分别得出方程求出答案;
(2)首先求出团购时总的费用,进而假设出儿童人数,利用不等式得出儿童人数的取值范围.
解答 解:(1)设每张成人票x元,每张儿童票y元.
根据题意,得$\left\{\begin{array}{l}{3x+y=350}\\{x+2y=200}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=100}\\{y=50}\end{array}\right.$.
∴每张成人票100元,每张儿童票50元.
(2)设参加旅游的儿童有m人,则成人有(30-m)人,
根据题意,得:
按团体票购买时总费用为100×80%×30=2 400元.
分别按成人票、儿童票购买时总费用为
100(30-m)+50m=3 000-50m.
①3 000-50m=2 400,解得m=12.
∴当儿童为12人时,两种购票方式花费相同.
②3 000-50m>2 400,解得m<12.
∴当儿童少于12人时,选择购买团体票花费少.
③3 000-50m<2 400,解得m>12.
∴当儿童多于12人时,选择分别按成人票、儿童票购票花费少.
点评 本题考查一元一次不等式及二元一次方程组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系,同时要注意分类讨论思想的运用.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目

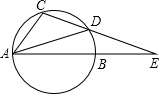 如图,⊙O的直径AB=2,C、D在⊙O上,AB与CD的延长线交于E 点,AC=CD,AD=DE,则劣弧AC的长为$\frac{2}{5}$π.
如图,⊙O的直径AB=2,C、D在⊙O上,AB与CD的延长线交于E 点,AC=CD,AD=DE,则劣弧AC的长为$\frac{2}{5}$π.