题目内容
6.某校九年级进行集体跳绳比赛.如图所示,跳绳时,绳甩到最高处时的形状可看作是某抛物线的一部分,记作G,绳子两端的距离AB约为8米,两名甩绳同学拿绳的手到地面的距离AC和BD基本保持1米,当绳甩过最低点时刚好擦过地面,且与抛物线G关于直线AB对称.(1)求抛物线G的表达式并写出自变量的取值范围;
(2)如果身高为1.5米的小华站在CD之间,且距点C的水平距离为m米,绳子甩过最高处时超过她的头顶,直接写出m的取值范围.

分析 (1)首先确定A、B和顶点E的坐标,然后利用待定系数法即可求得函数的解析式;
(2)求得当y=1.5时,对应的x的值,则m的范围即可求得.
解答 解:(1)如图所示建立平面直角坐标系.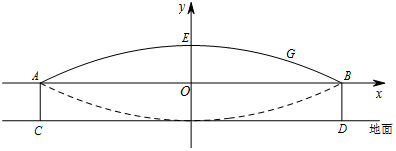
由题意可知A(-4,0),B(4,0),顶点E(0,1).
设抛物线G的表达式为y=ax2+1.
∵A(-4,0)在抛物线G上,
∴16a+1=0,解得$a=-\frac{1}{16}$.
∴$y=-\frac{1}{16}{x^2}+1$.
自变量的取值范围为-4≤x≤4.
(2)当y=1.5-1=0.5时,-$\frac{1}{16}$x2+1=0.5,
解得:x=±4$\sqrt{2}$,
∴m的取值范围是:4-4$\sqrt{2}$<m<4+4$\sqrt{2}$.
点评 本题考查了待定系数法求函数的解析式,以及二次函数的实际应用,此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
7.桌面上放置的几何体中,主视图与左视图可能不同的是( )
| A. | 圆柱 | B. | 正方体 | C. | 球 | D. | 直立圆锥 |
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b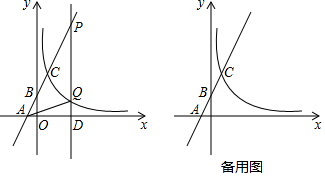
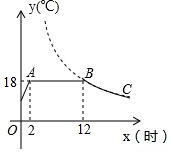 如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.
如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃. 如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.
如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.