题目内容
7.一次函数y=kx+b的图象与两坐标轴分别交于A(2,0),B(0,-1)两点.(1)求k、b;
(2)P为该一次函数图象上一点,过P作PQ⊥x轴,垂足为Q.若S△PAQ=4,求点P的坐标.
分析 (1)把A(2,0)B(0,-1)代入y=kx+b即可得到结论;
(2)由y=$\frac{1}{2}$x-1,可设P1(x,$\frac{1}{2}$x-1),于是得到AQ=x-2,P1Q1=$\frac{1}{2}$x-1.根据已知条件得到(x-2)($\frac{1}{2}$x-1)=4×2.于是得到结论.
解答 解:(1)由A(2,0)B(0,-1)得$\left\{\begin{array}{l}0=2k+b\\-1=b\end{array}$,
∴$\left\{\begin{array}{l}k=\frac{1}{2}\\ b=-1\end{array}$;
(2)由y=$\frac{1}{2}$x-1,可设P1(x,$\frac{1}{2}$x-1),
∴AQ=x-2,P1Q1=$\frac{1}{2}$x-1.
∴(x-2)($\frac{1}{2}$x-1)=4×2.
x1=-2(舍),x2=6.
∴P1(6,2).
∵△P2Q2A≌△P1Q1A,
∴AQ2=AQ1=4.
∴OQ=2.
∴P2(-2,-2).
∴P1(6,2),P2(-2,-2).
点评 此题考查了一次函数图象上点的坐标问题,利用了待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 同圆或等圆中,等现所对的圆周角相等 | |
| B. | 圆的切线垂直于半径 | |
| C. | 三角形的内心是三角形角平分线的交点 | |
| D. | 平分弦的直径垂直于弦 |
 如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.
如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.
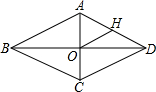 如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.
如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.