题目内容
3.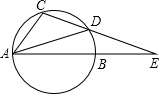 如图,⊙O的直径AB=2,C、D在⊙O上,AB与CD的延长线交于E 点,AC=CD,AD=DE,则劣弧AC的长为$\frac{2}{5}$π.
如图,⊙O的直径AB=2,C、D在⊙O上,AB与CD的延长线交于E 点,AC=CD,AD=DE,则劣弧AC的长为$\frac{2}{5}$π.
分析 连接BC、OC,设∠E=α,求出∠DAE=∠E=α,∠ADC=2α,∠ABC=∠CAD=∠ADC=2α,根据∠ACB=90°求出5α=90°,求出∠AOC=72°,根据弧长公式求出即可.
解答 解:连接BC,OC,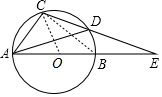
设∠E=α,
∵AD=DE,
∴∠DAE=∠E=α,∠ADC=∠E+∠DAE=2α,
∴∠ABC=∠CAD=∠ADC=2α,
∵AB是☉O的直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
即5α=90°,
∴∠E=18°,
∴∠AOC=72°,
劣弧AC的长=$\frac{72×π×1}{180}$=$\frac{2}{5}$π,
故答案为:$\frac{2}{5}$π.
点评 本题考查了圆周角定理,弧长公式等知识点,能求出∠AOC的度数是解此题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b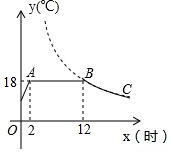 如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.
如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃. 如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.
如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.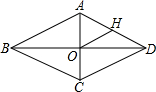 如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.
如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.