题目内容
1. 在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴相交于点A和点B,已知点A的坐标为(1,0),与y轴相交于点C(0,3),抛物线的顶点为P.
在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴相交于点A和点B,已知点A的坐标为(1,0),与y轴相交于点C(0,3),抛物线的顶点为P.(1)求这条抛物线的解析式,并写出顶点P的坐标;
(2)如果点D在此抛物线上,DF⊥x轴于点F,DF与直线PB相交于点E,设点D的横坐标为t(t>3),且DE:EF=2:1,求点D的坐标;
(3)在第(2)小题的条件下,求证:∠DPE=∠BDE.
分析 (1)将A(1,0)、C(0,3)代入抛物线的解析式可求得关于b、c的方程组,解得b、c的值可求得抛物线的解析式,最后依据配方法可求得抛物线的顶点坐标;
(2)过点P作PG⊥AB,垂足为G.先求得点B的坐标,由点B和点P的坐标可知△PBG为等腰直角三角形,从而可证明△BEF为等腰直角三角形,设点D的坐标为(t,t2-4t+3),然后求得EF,DF的长(用含t的式子表示),最后根据PF与EF的数量关系列出关于t的一元二次方程,从而可求得t的值;
(3)先求得DE,BE,PE的长,接下来再证明DE2=BE•PE,从而可得到EBD∽△EDP,最后依据相似三角形的性质可求得∠DPE=∠BDE.
解答 解:(1)∵将A(1,0)、C(0,3)代入得:$\left\{\begin{array}{l}{c=3}\\{1+b+c=0}\end{array}\right.$,
解得:b=-4,c=3.
∴抛物线的解析式为y=x2-4x+3.
∵y=x2-4x+3=(x-2)2-1,
∴点P的坐标为(2,-1).
(2)过点P作PG⊥AB,垂足为G.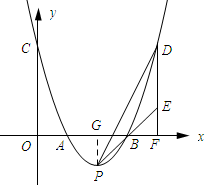
∵令y=0得:x2-4x+3=0,解得x1=1,x2=3,
∴B(3,0).
又∵P(2,-1),
∴PG=BG=1.
∴∠GBP=45°.
∴∠EBF=45°.
又∵∠EFB=90°,
∴∠EBF=∠FEB=45°.
∴BF=EF.
设D(t,t2-4t+3),则DF=t2-4t+3,则BF=T-3.
∵DE:EF=2:1,
∴DF=3EF=3(t-3).
∴t2-4t+3=3(t-3).
解得:t1=4,t2=3(舍去).
∴D(4,3).
(3)∵t=4,
∴EF=BF=4-3=1.
∴点E的坐标为(4,1).
∴BE=$\sqrt{B{F}^{2}+E{F}^{2}}$=$\sqrt{2}$,ED=DF-EF=3-1=2,PE=$\sqrt{(4-2)^{2}+(-1-1)^{2}}$=2$\sqrt{2}$.
∴DE2=22=4,BE•PE=$\sqrt{2}×2\sqrt{2}$=4.
∴DE2=BE•PE.
又∵∠DEB=∠PED,
∴△EBD∽△EDP.
∴∠DPE=∠BDE.
点评 本题主要考查的是二次函数的综合应用,解答本题主要利用了待定系数法求二次函数的解析式、等腰直角三角形的性质和判定、一元二次方程的解法、勾股定理以及相似三角形的性质和判定,证得DE2=BE•PE从而得到△EBD∽△EDP是解题的关键.

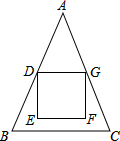 如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )
如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )| A. | 1 | B. | 2 | C. | $\sqrt{21}$ | D. | $\sqrt{29}$ |
①函数图象开口向上
②无论k取何值时,函数图象总交于y轴的正半轴
③无论k取何值时,函数图象与x轴的交点间的距离为1
④当k>$-\frac{3}{2}$时,图象的顶点在第四象限.
| A. | ①②③④ | B. | ①③④ | C. | ①③ | D. | ①④ |
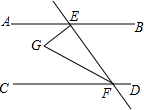 如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )
如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
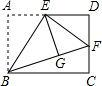 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4$\sqrt{6}$,则FD的长为4.
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4$\sqrt{6}$,则FD的长为4.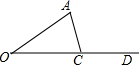 如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.
如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.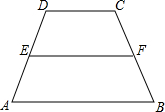 如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).
如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).