题目内容
11.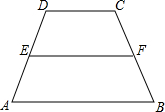 如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).
如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).
分析 由在梯形△ABCD中,E、F分别为腰AD、BC的中点,可得$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{DC}$),继而求得答案.
解答 解:∵在梯形△ABCD中,E、F分别为腰AD、BC的中点,
∴$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{DC}$),
∵$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,
∴$\overrightarrow{AB}$=2$\overrightarrow{EF}$-$\overrightarrow{DC}$=10$\overrightarrow{m}$-3$\overrightarrow{m}$=7$\overrightarrow{m}$.
故答案为:7$\overrightarrow{m}$.
点评 此题考查了平面向量的知识以及梯形的中位线的性质.注意梯形的中位线平行于上下底,且等于上底与下底和的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.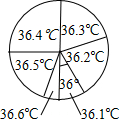 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )| 体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
| 人数(人) | 4 | 8 | 8 | 10 | x | 2 |
| A. | 这些体温的众数是8 | B. | 这些体温的中位数是36.35 | ||
| C. | 这个班有40名学生 | D. | x=8 |
16.已知n是使$\sqrt{27n}$的值为整数的最小正整数,估算$\sqrt{n}$的值,下列说法正确的是( )
| A. | 在1和2之间 | B. | 在2和3之间 | C. | 在3和4之间 | D. | 在4和5之间 |
 在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴相交于点A和点B,已知点A的坐标为(1,0),与y轴相交于点C(0,3),抛物线的顶点为P.
在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴相交于点A和点B,已知点A的坐标为(1,0),与y轴相交于点C(0,3),抛物线的顶点为P.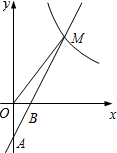 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2. 如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为H,AD的中点E的对应点记为G,若△GFH∽△GBF,则AD=$\frac{16}{5}$.
如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为H,AD的中点E的对应点记为G,若△GFH∽△GBF,则AD=$\frac{16}{5}$.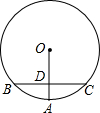 如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.
如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.