题目内容
9.阅读:你会解一元二次不等式吗?请阅读下面的解题过程吧!解不等式(x-3)(x+1)<0.
解:将(x-3)和(x+1)分别看作两个整体,根据“异号两数相乘,积为负数”可知,原不等式可转化为$\left\{\begin{array}{l}{x-3>0}\\{x+1<0}\end{array}\right.$或$\left\{\begin{array}{l}{x-3<0}\\{x+1>0}\end{array}\right.$,分别解两个不等式组,的$\left\{\begin{array}{l}{x>3}\\{x<-1}\end{array}\right.$或$\left\{\begin{array}{l}{x<3}\\{x>-1}\end{array}\right.$,所以原不等式解集为-1<x<3.
试用上述方法,解不等式($\frac{2}{3}$x-3)•[5(x-1)+1]>0.
分析 根据题意得出两式为同号,进而利用两式同时大于0或同时小于0列出不等式组,进而得出答案.
解答 解:∵($\frac{2}{3}$x-3)•[5(x-1)+1]>0,
∴$\left\{\begin{array}{l}{\frac{2}{3}x-3>0}\\{5(x-1)+1>0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{2}{3}x-3<0}\\{5(x-1)+1<0}\end{array}\right.$,
解得:x>4.5或x<0.8.
点评 此题主要考查了一元一次不等式组的应用,一元二次不等式的解法,利用分类讨论得出是解题关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
19.七边形的内角和是( )
| A. | 1 260度 | B. | 1 080度 | C. | 900度 | D. | 720度 |
 如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB,交CB的延长线于G.
如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB,交CB的延长线于G. 如图,四边形OABC和ADEF均为正方形,反比例函数y=$\frac{8}{x}$的图象分别经过AB的中点M及DE的中点N,则正方形ADEF的边长为-2+2$\sqrt{5}$.
如图,四边形OABC和ADEF均为正方形,反比例函数y=$\frac{8}{x}$的图象分别经过AB的中点M及DE的中点N,则正方形ADEF的边长为-2+2$\sqrt{5}$.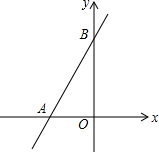 如图,直线y=2x+3与x轴交于点A,与y轴交于点B.
如图,直线y=2x+3与x轴交于点A,与y轴交于点B.