题目内容
18.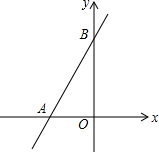 如图,直线y=2x+3与x轴交于点A,与y轴交于点B.
如图,直线y=2x+3与x轴交于点A,与y轴交于点B.(1)求A,B两点的坐标;
(2)过点B作直线BP与x轴交于点P,使S△BPO=2S△ABP,求直线BP的解析式.
分析 (1)利用坐标轴上点的特征确定A,B两点的坐标;
(2)利用三角形面积公式得到OP=2AP,即点A为OP的中点,则P(-3,0),然后利用待定系数法求PB的解析式.
解答 解:(1)当y=0时,2x+3=0,解得x=-$\frac{3}{2}$,则A(-$\frac{3}{2}$,0),
当x=0时,y=2x+3=3,则B(0,3);
(2)∵S△BPO=2S△ABP,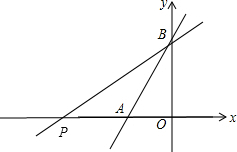
∴OP=2AP,
即点A为OP的中点,
∴P(-3,0),
设直线PB的解析式为y=kx+b,如图,
把P(-3,0),B(0,3)代入得$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线PB的解析式为y=x+3.
点评 本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了待定系数法求一次函数解析式.

练习册系列答案
相关题目
7. 如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
 如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )| A. | 2条 | B. | 4条 | C. | 8条 | D. | 无数条 |
 在棋盘中建立如图所示的平面直角坐标系,三颗棋子A,O,B的位置如图所示,它们的坐标分别是(-1,1),(0,0)和(1,0)
在棋盘中建立如图所示的平面直角坐标系,三颗棋子A,O,B的位置如图所示,它们的坐标分别是(-1,1),(0,0)和(1,0) 如图,
如图,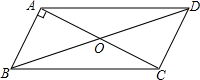 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,则BD=2$\sqrt{2}$.
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,则BD=2$\sqrt{2}$.