Question

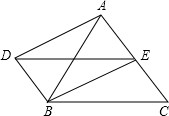
在△ABC中，∠ACB=90°，BC的垂直平分线交AB于D，垂足为E．
（1）若∠A=60°，则∠DCB=

 

，∠ADC=

 

；     
（2）若∠B=30°，BD=5，求△ACD的周长．

Answer 1

考点：线段垂直平分线的性质,含30度角的直角三角形,直角三角形斜边上的中线

专题：

分析：（1）先根据直角三角形的性质求出∠B的度数，再根据线段垂直平分线的性质得出CD=BD，故可得出∠DCB的度数，由三角形外角的性质即可得出∠ADC的度数；
（2）先根据BD=5得出CD=5，再根据∠B=30°得出∠A的度数，判断出△ACD的形状，进而可得出结论．

解答：解：（1）∵在△ABC中，∠ACB=90°，∠A=60°，
∴∠B=30°．
∵BC的垂直平分线交AB于D，垂足为E，
∴CD=BD，
∴∠DCB=∠B=30°．
∵∠ADC是△BCD的外角，
∴∠ADC=∠B+∠DCB=30°+30°=60°．
故答案为：30°，60°；
（2）∵BC的垂直平分线交AB于D，垂足为E，∠B=30°，BD=5，
∴CD=BD=5，∠DCB=30°．
∵∠ACB=90°，
∴∠A=90°-30°=60°，∠ACD=90°-∠DCB=90°-30°=60°，
∴△ACD是等边三角形，
∴△ACD的周长=3CD=3×5=15．

点评：本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．