题目内容
2.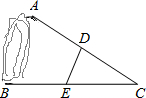 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )| A. | 280米 | B. | 300米 | C. | 420米 | D. | 无法确定 |
分析 先判断出DE是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得AB=2DE,问题得解.
解答 解:∵点D,E分别是BC和AC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×210=420米.
故选C.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,熟记定理并准确识图是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
12.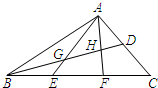 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{10}$ | C. | $\frac{6}{11}$ | D. | $\frac{11}{20}$ |
17.下面是石林县某校八年级(1)班七位女同学的体重(单位:kg):51 50 40 43 48 48 63,这组数据的众数和中位数分别是( )
| A. | 48,43 | B. | 48,48 | C. | 43,48 | D. | 48,49 |
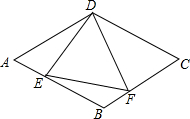 如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.
如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.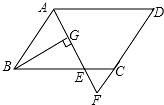 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求:
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求: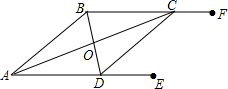 如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证: