题目内容
3.观察一组等式的规律:1×3+1=22,2×4+1=32,3×5+1=42,4×6+1=52…,则第n个等式为:n(n+2)+1=(n+1)2.分析 根据1×3+1=22,2×4+1=32,3×5+1=42,4×6+1=52…,判断出每个加数、和的特征,求出第n个等式即可.
解答 解:∵1×3+1=22,2×4+1=32,3×5+1=42,4×6+1=52…,
∴第n个等式为:n(n+2)+1=(n+1)2.
故答案为:n(n+2)+1=(n+1)2.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律.

练习册系列答案
相关题目
18.如图所示,用1个边长为c的小正方形和直角边长分别为a,b的4个直角三角形,恰好能拼成一个新的大正方形,其中a,b,c满足等式c2=a2+b2,由此可验证的乘法公式是( )


| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | (a+b)(a-b)=a2-b2 | D. | a2+b2=(a+b)2 |
13.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{16}$ | B. | $\sqrt{6}$ | C. | $\sqrt{28}$ | D. | $\sqrt{\frac{1}{5}}$ |
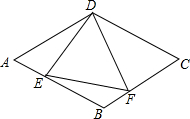 如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.
如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.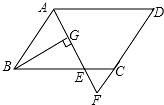 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求:
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求: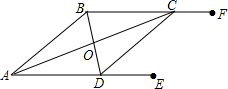 如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证: