题目内容
10.(1)解方程:x2-2x-3=0(2)计算:(π-$\sqrt{3}$)0+($\frac{1}{2}$)-1-$\sqrt{27}$-tan60°.
分析 (1)方程利用因式分解法求出解即可;
(2)原式利用零指数幂、负整数指数幂,以及特殊角的三角函数值计算即可得到结果.
解答 解:(1)分解得:(x-3)(x+1)=0,
可得x-3=0或x+1=0,
解得:x1=3,x2=-1;
(2)原式=1+2-3$\sqrt{3}$-$\sqrt{3}$=3-4$\sqrt{3}$.
点评 此题考查了实数的运算,以及解一元二次方程-因式分解法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
15.某楼盘商品房成交价今年3月份为a元/m3,4月份比3月份减少了8%,若4月份到6月份平均增长率为12%,则6月份商品房成交价是( )
| A. | a(1-8%)(1+12%)元 | B. | a(1-8%)(1+12%)2元 | C. | (a-8%)(a+12%)元 | D. | a(1-8%+12%)元 |
 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.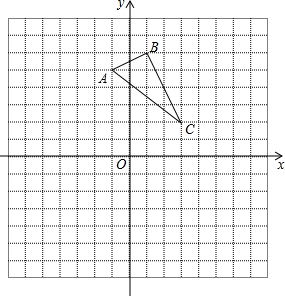 已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.
已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.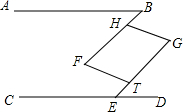 如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.
如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.
 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,连接BF交AC、DC、DE分别为P、Q、R.
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,连接BF交AC、DC、DE分别为P、Q、R.