题目内容
4.一个等腰三角形有两边长是关于x的方程x2-17x+m=0的两根,其中一条边长是9.求这个三角形的周长.分析 由于一个等腰三角形的一边长为9,另两边长是关于x的方程x2-17x+m=0的两根,由根与系数的关系知x1+x2=17,有两种情况:
①当腰长为9时,然后求出方程的另一根,也就可以求出三角形的周长;
②当底边为9时,方程的另一根为腰,也就可以求出三角形的周长.
解答 解:由根与系数的关系知x1+x2=17,其中有一边长为9,则另一边长为17-9=8.
(1)若腰长为9,则周长为9+9+8=26;
(2)若底边长为9,则周长为8+8+9=25.
点评 此题考查根与系数的关系,等腰三角形的性质,分两种情况探讨是解决问题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
14.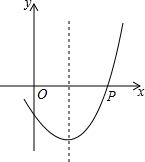 如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )
如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )
 如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )
如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )| A. | abc<0 | B. | 2a+b<0 | C. | 3a+c<0 | D. | 4a-2b+c>0 |
9.计算$\frac{6{x}^{2}}{{x}^{2}-x}•\frac{{x}^{2}-1}{3x}$的结果是( )
| A. | 2x+2 | B. | 2x-2 | C. | 2x2+2x | D. | 2x2-2x |
