题目内容
15.解方程(1)x2-2$\sqrt{2}$x+2=0(公式法)
(2)3x(5x-2)=4-25x2.
分析 (1)由方程可知a=1,b=-2$\sqrt{2}$,c=2,b2-4ac=8-8=0,然后利用公式可解方程;
(2)先将方程化简整理为10x2-6x-4=0,然后利用因式分解法解得方程.
解答 解:(1)∵x2-2$\sqrt{2}$x+2=0,
∴a=1,b=-2$\sqrt{2}$,c=2,b2-4ac=8-8=0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2\sqrt{2}±0}{2}$=$\sqrt{2}$,
x1=x2=$\sqrt{2}$;
(2)∵3x(5x-2)=4-25x2,
∴15x2-6x=4-25x2,
∴10x2-6x-4=0,
∴(5x+2)(x-1)=0,
∴5x+2=0或x-1=0,
∴x1=1,x2=-$\frac{2}{5}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
6.已知∠A=32°18′,则∠A的余角为( )
| A. | 57°42′ | B. | 57°82′ | C. | 147°42′ | D. | 147°82′ |
3.2015年亚洲杯足球冠军联赛恒大队广州主场,小李在网上预订了小组赛和淘汰赛两个阶段的球票共10张,总价为5600元.其中小组赛球票每张500元,淘汰赛每张800元,问小李预定了小组赛和淘汰赛的球票各多少张?设小李预定了小组赛球票x张,淘汰赛球票y张,可列方程组( )
| A. | $\left\{\begin{array}{l}x+y=5600\\ 500x+800y=10\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=10\\ 800x+500y=5600\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=10\\ 500x+800y=5600\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=10\\ 500x-800y=5600\end{array}\right.$ |
10.迎接学校“元旦”文艺汇演,八年级某班的全体同学捐款购买了表演道具,经过充分的排练准备,最终获得了一等奖.班长对全体同学的捐款情况绘制成下表:
由于填表时不小心把墨水滴在了统计表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的30%,结合上表回答下列问题:
(1)该班共有50名同学;
(2)该班同学捐款金额的众数是15元,中位数是12.5元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为
36度.
| 捐款金额 | 5元 | 10元 | 15元 | 20元 |
| 捐款人数 | 10人 | 15人 |  | 5人 |
(1)该班共有50名同学;
(2)该班同学捐款金额的众数是15元,中位数是12.5元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为
36度.
5.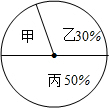 某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
 某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )| A. | 甲对应扇形的圆心角为72° | B. | 学生的总人数是900人 | ||
| C. | 甲比丙地区人数少180人 | D. | 丙比乙地区人数多180人 |
 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.