题目内容
14.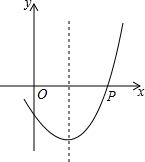 如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )
如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )| A. | abc<0 | B. | 2a+b<0 | C. | 3a+c<0 | D. | 4a-2b+c>0 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:A、根据图示知,抛物线开口方向向上,则a>0.
抛物线的对称轴x=-$\frac{b}{2a}$=1>0,则b<0.
抛物线与y轴交与负半轴,则c<0,
所以abc>0.
故本选项错误;
B、∵x=-$\frac{b}{2a}$=1,
∴b=-2a,
∴2a+b=0,
故本选项错误;
C、∵对称轴为直线x=1,图象经过(3,0),
∴该抛物线与x轴的另一交点的坐标是(-1,0),
∴当x=-1时,y=0,即a-b+c=0.
∵b=-2a,
∴a+2a+c=0,
∴3a+c=0,故本选项错误;
D、根据图示知,当x=-2时,y>0,即4a-2b+c>0,故本选项正确;
故选:D.
点评 本题考查了二次函数图象与系数的关系,熟练利用二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴判断得出是解题关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
4.平面直角坐标系内有一点A(a,-a),若a>0,则点A位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知关于x的方程x2+mx-2=0的一个根是-1,则m的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 0或1 |
6.已知∠A=32°18′,则∠A的余角为( )
| A. | 57°42′ | B. | 57°82′ | C. | 147°42′ | D. | 147°82′ |
3.2015年亚洲杯足球冠军联赛恒大队广州主场,小李在网上预订了小组赛和淘汰赛两个阶段的球票共10张,总价为5600元.其中小组赛球票每张500元,淘汰赛每张800元,问小李预定了小组赛和淘汰赛的球票各多少张?设小李预定了小组赛球票x张,淘汰赛球票y张,可列方程组( )
| A. | $\left\{\begin{array}{l}x+y=5600\\ 500x+800y=10\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=10\\ 800x+500y=5600\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=10\\ 500x+800y=5600\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=10\\ 500x-800y=5600\end{array}\right.$ |
 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.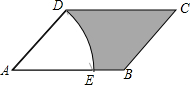 如图,在平行四边形ABCD中,∠A=45°,以A为圆心,AD为半径画弧交AB于E,AD=2,EB=1,则图中阴影部分的面积是3$\sqrt{2}$-$\frac{1}{2}$π(保留π).
如图,在平行四边形ABCD中,∠A=45°,以A为圆心,AD为半径画弧交AB于E,AD=2,EB=1,则图中阴影部分的面积是3$\sqrt{2}$-$\frac{1}{2}$π(保留π).