题目内容
5.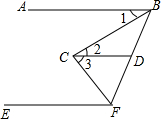 已知,AB∥CD∥EF,且CB平分∠ABF,CF平分∠BEF,请说明BC⊥CF的理由.
已知,AB∥CD∥EF,且CB平分∠ABF,CF平分∠BEF,请说明BC⊥CF的理由.解:∵AB∥E(已知)
∴∠ABF+∠BFE=,180°.
∵CB平分∠ABF(已知)
∴∠1=$\frac{1}{2}$∠ABF
同理,∠4=$\frac{1}{2}$∠BEF
∴∠1+∠4=$\frac{1}{2}$(∠ABF+∠BEF)=90°.
又∵AB∥CD (已知)
∴∠1=∠2两直线平行,内错角相等
同理,∠3=∠4
∴∠1+∠4=∠2+∠3等式的性质
∴∠2+∠3=90°(等量代换)
即∠BCF=90°
∴BC⊥CF垂直的定义.
分析 根据平行线的性质得到∠ABF+∠BFE=180°.由角平分线的定义得到∠1=$\frac{1}{2}$∠ABF,∠4=$\frac{1}{2}$∠BEF,根据平行线的性质得到∠1=∠2,同理,∠3=∠4,根据垂直的定义即可得到结论.
解答 解:∵AB∥E(已知)
∴∠ABF+∠BFE=180°.
∵CB平分∠ABF(已知)
∴∠1=$\frac{1}{2}$∠ABF
同理,∠4=$\frac{1}{2}$∠BEF
∴∠1+∠4=$\frac{1}{2}$(∠ABF+∠BEF)=90°.
又∵AB∥CD (已知)
∴∠1=∠2(两直线平行,内错角相等),
同理,∠3=∠4
∴∠1+∠4=∠2+∠3(等式的性质),
∴∠2+∠3=90°(等量代换)
即∠BCF=90°
∴BC⊥CF(垂直的定义).
故答案为:ABF,BFE,180°,90°,两直线平行,内错角相等,等式的性质,垂直的定义.
点评 本题考查了平行线的性质,角平分线的定义,垂直的定义,熟练掌握各性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,菱形ABCD中,AC与BD交于点O.∠ADC=120°,BD=2,则AC的长为( )
如图,菱形ABCD中,AC与BD交于点O.∠ADC=120°,BD=2,则AC的长为( )
 如图,菱形ABCD中,AC与BD交于点O.∠ADC=120°,BD=2,则AC的长为( )
如图,菱形ABCD中,AC与BD交于点O.∠ADC=120°,BD=2,则AC的长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
1.下列命题中,不正确的是( )
| A. | 两条直线相交形成的对顶角一定相等 | |
| B. | 两条平行线被第三条直线所截,同旁内角一定相等 | |
| C. | 三角形的第三边一定大于另两边之差并且小于另两边之和 | |
| D. | 三角形一边上的高的长度一定不大于这条边上的中线的长度 |
8. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F. 如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.
如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.