题目内容
3.在△ABC中,AB=2,AC=$\sqrt{2}$,以A为圆心,1为半径的圆与BC边所在的直线相切,则∠BAC的度数是15°或105°.分析 首先通过作辅助线构建直角三角形,然后分别得出三角形各内角度数,进而得出答案.
解答 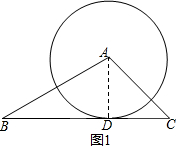 解:如图1,设圆A与BC切于点D,连接AD,
解:如图1,设圆A与BC切于点D,连接AD,
则AD⊥BC,
在直角△ABD中,AB=2,AD=1,则sinB=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴∠B=30°,
∴∠BAD=60°,
同理,在直角△ACD中,tanC=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
得到∠CAD=45°,
因而∠BAC的度数是105°.
如图2,设圆A与BC延长线切于点D,连接AD,
则AD⊥BC,
在直角△ABD中,AB=2,AD=1,则sinB=$\frac{AD}{AB}$=$\frac{1}{2}$,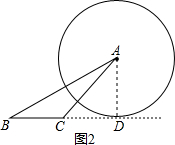
∴∠B=30°,
∴∠BAD=60°,
同理,在直角△ACD中,tan∠ACD=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
得到∠CAD=45°,
因而∠BAC的度数是15°.
故答案为:15°或105°.
点评 此题主要考查了切线的性质以及锐角三角函数关系,通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题是解题关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
11. 如图,在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,下面结论错误的是( )
如图,在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,下面结论错误的是( )
 如图,在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,下面结论错误的是( )
如图,在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,下面结论错误的是( )| A. | △ABM≌△CDN | B. | AC=3AM | C. | DN=2NF | D. | BM=3ME |
8. 用尺规作∠AOB平分线的方法如下:①以点O为圆心,任意长为半径作弧交OA,OB于点C,点D;②分别以点C,点D为圆心,以大于$\frac{1}{2}$CD长为半径作弧,两弧交于点P;③作射线OP,则OP平分∠AOB,由作法得△OCP≌△ODP,其判定的依据是( )
用尺规作∠AOB平分线的方法如下:①以点O为圆心,任意长为半径作弧交OA,OB于点C,点D;②分别以点C,点D为圆心,以大于$\frac{1}{2}$CD长为半径作弧,两弧交于点P;③作射线OP,则OP平分∠AOB,由作法得△OCP≌△ODP,其判定的依据是( )
 用尺规作∠AOB平分线的方法如下:①以点O为圆心,任意长为半径作弧交OA,OB于点C,点D;②分别以点C,点D为圆心,以大于$\frac{1}{2}$CD长为半径作弧,两弧交于点P;③作射线OP,则OP平分∠AOB,由作法得△OCP≌△ODP,其判定的依据是( )
用尺规作∠AOB平分线的方法如下:①以点O为圆心,任意长为半径作弧交OA,OB于点C,点D;②分别以点C,点D为圆心,以大于$\frac{1}{2}$CD长为半径作弧,两弧交于点P;③作射线OP,则OP平分∠AOB,由作法得△OCP≌△ODP,其判定的依据是( )| A. | ASA | B. | SAS | C. | AAS | D. | SSS |
12. 如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )
 如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,已知∠B+∠BCD=180°,∠B=∠D.
如图,已知∠B+∠BCD=180°,∠B=∠D. 作图题:求作⊙P,使⊙P 满足以线段MN为弦且圆心P到OA及OB边的距离相等.(保留作图轨迹)
作图题:求作⊙P,使⊙P 满足以线段MN为弦且圆心P到OA及OB边的距离相等.(保留作图轨迹)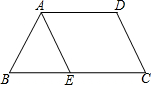 如图,已知梯形ABCD中,AD∥BC,点E在BC边上,AE∥DC,DC=AB.如果图中的线段都是有向线段,则与$\overrightarrow{AE}$相等的向量是$\overrightarrow{DC}$.
如图,已知梯形ABCD中,AD∥BC,点E在BC边上,AE∥DC,DC=AB.如果图中的线段都是有向线段,则与$\overrightarrow{AE}$相等的向量是$\overrightarrow{DC}$.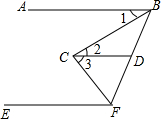 已知,AB∥CD∥EF,且CB平分∠ABF,CF平分∠BEF,请说明BC⊥CF的理由.
已知,AB∥CD∥EF,且CB平分∠ABF,CF平分∠BEF,请说明BC⊥CF的理由.