题目内容
4. 如图,菱形ABCD中,AC与BD交于点O.∠ADC=120°,BD=2,则AC的长为( )
如图,菱形ABCD中,AC与BD交于点O.∠ADC=120°,BD=2,则AC的长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 根据菱形的性质可得BD平分∠ADC,BO=DO=$\frac{1}{2}$BD,BD⊥AC,AO=CO=$\frac{1}{2}$AC,然后根据直角三角形的性质计算出AD长,再利用勾股定理可得AO长,进而可得答案.
解答 解:∵四边形ABCD是菱形,
∴BD平分∠ADC,BO=DO=$\frac{1}{2}$BD,BD⊥AC,AO=CO=$\frac{1}{2}$AC,
∵∠ADC=120°,
∴∠ADB=60°,
∴∠DAO=30°,
∵BD=2,
∴DO=1,AD=2,
∴AO=$\sqrt{A{D}^{2}-D{O}^{2}}$=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
故选:D.
点评 此题主要考查了菱形的性质,关键是掌握菱形对角线互相平分、垂直且平分每一组对角,菱形四边形相等.

练习册系列答案
相关题目
12. 如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )
 如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A,B,C三点,CA⊥CB于点C,∠1=30°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
19.下列的三条线段能组成三角形的是( )
| A. | 1,2,3 | B. | 2,2,4 | C. | 3,4,5 | D. | 3,4,8 |
 作图题:求作⊙P,使⊙P 满足以线段MN为弦且圆心P到OA及OB边的距离相等.(保留作图轨迹)
作图题:求作⊙P,使⊙P 满足以线段MN为弦且圆心P到OA及OB边的距离相等.(保留作图轨迹)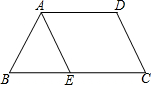 如图,已知梯形ABCD中,AD∥BC,点E在BC边上,AE∥DC,DC=AB.如果图中的线段都是有向线段,则与$\overrightarrow{AE}$相等的向量是$\overrightarrow{DC}$.
如图,已知梯形ABCD中,AD∥BC,点E在BC边上,AE∥DC,DC=AB.如果图中的线段都是有向线段,则与$\overrightarrow{AE}$相等的向量是$\overrightarrow{DC}$. 如图是“赵爽弦图”,△ABH、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AH=6,EF=2,那么AB等于10.
如图是“赵爽弦图”,△ABH、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AH=6,EF=2,那么AB等于10.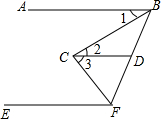 已知,AB∥CD∥EF,且CB平分∠ABF,CF平分∠BEF,请说明BC⊥CF的理由.
已知,AB∥CD∥EF,且CB平分∠ABF,CF平分∠BEF,请说明BC⊥CF的理由.