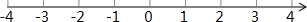题目内容
8.从-2,-1,0,1,2这5个数中,随机抽取一个数记为a,则使关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-1}{6}≥-\frac{1}{2}}\\{2x-1<2a}\end{array}\right.$有解,且使关于x的一元一次方程$\frac{3x-a}{2}$+1=$\frac{2x+a}{3}$的解为负数的概率为$\frac{3}{5}$.分析 分别求得使关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-1}{6}≥-\frac{1}{2}}\\{2x-1<2a}\end{array}\right.$有解,且使关于x的一元一次方程$\frac{3x-a}{2}$+1=$\frac{2x+a}{3}$的解为负数的a的值满足的条件,然后利用概率公式求解即可.
解答 解:∵使关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-1}{6}≥-\frac{1}{2}}\\{2x-1<2a}\end{array}\right.$有解的a满足的条件是a>-$\frac{3}{2}$,
使关于x的一元一次方程$\frac{3x-a}{2}$+1=$\frac{2x+a}{3}$的解为负数的a的a<$\frac{6}{5}$,
∴使关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-1}{6}≥-\frac{1}{2}}\\{2x-1<2a}\end{array}\right.$有解,且使关于x的一元一次方程$\frac{3x-a}{2}$+1=$\frac{2x+a}{3}$的解为负数的a的值为-1,0,1,三个数,
∴使关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-1}{6}≥-\frac{1}{2}}\\{2x-1<2a}\end{array}\right.$有解,且使关于x的一元一次方程$\frac{3x-a}{2}$+1=$\frac{2x+a}{3}$的解为负数的概率为$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题考查了概率公式、一元一次方程的解及解一元一次不等式组的知识,解题的关键是首先确定满足条件的a的值,难度不大.

 阅读快车系列答案
阅读快车系列答案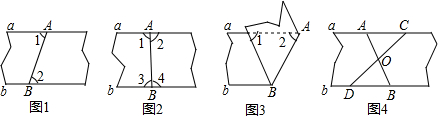
| A. | 如图1,展开后测得∠1=∠2 | |
| B. | 如图2,展开后测得∠1=∠2且∠3=∠4 | |
| C. | 如图3,测得∠1=∠2 | |
| D. | 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD |
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 两个根都是自然数 | D. | 无实数根 |
| A. | -$\frac{1}{x-1}$ | B. | $\frac{1}{1+x}$ | C. | -$\frac{1}{1+x}$ | D. | $\frac{1}{x-1}$ |
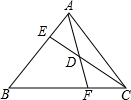 已知D为AF的中点,BF=2FC,求AE:BE的值.
已知D为AF的中点,BF=2FC,求AE:BE的值.