题目内容
18．
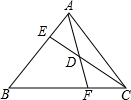已知D为AF的中点，BF=2FC，求AE：BE的值．
分析 过F点作FG∥AB，如图，由FG∥AE，根据平行线分线段成比例得$\frac{FG}{AE}$=$\frac{DF}{DA}$，则利用D为AF的中点得到FG=AE，再利用FG∥BE得到$\frac{FG}{BE}$=$\frac{FC}{BC}$，则利用BC=3CF可得BE=3FG，然后可计算出AE：BE=1：3．
解答 解：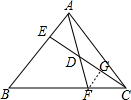
过F点作FG∥AB，如图，
∵FG∥AE，
∴$\frac{FG}{AE}$=$\frac{DF}{DA}$，
而D为AF的中点，
∴FG=AE，
∵FG∥BE，
∴$\frac{FG}{BE}$=$\frac{FC}{BC}$，
而BF=2FC，
∴BC=3CF，
∴BE=3FG，
∴AE：BE=FG：3FG=1：3．
点评 本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
练习册系列答案
相关题目
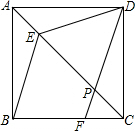如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线于点P，且DE=DP．
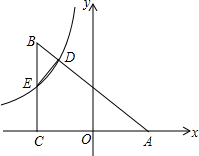如图，△ABC顶点A在x轴上，∠BCA=90°，AC=4，BC=3，反比例函数y=-$\frac{4}{3x}$（x＜0）的图象分别与AB，BC交于点D，E．设点E、D的横坐标分别为a、b，连结DE，当△BDE∽△BCA时，a、b的关系式为b=$\frac{1}{a}$．
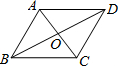如图，四边形ABCD是平行四边形，AC与BD相交于点O，添加一个条件：AB=BC或AC⊥BD等，可使它成为菱形．
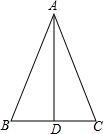如图，在△ABC中，AB=AC，AD是边BC上的高，求证：
一个工件，外部是圆柱体，内部凹槽是正方体，如图所示，其中，正方体一个面的四个顶点都在圆柱底面的圆周上，若圆柱底面周长为2πcm，则正方体的体积为2$\sqrt{2}$cm3．