题目内容
13.分式-$\frac{1}{1-x}$可变形为( )| A. | -$\frac{1}{x-1}$ | B. | $\frac{1}{1+x}$ | C. | -$\frac{1}{1+x}$ | D. | $\frac{1}{x-1}$ |
分析 先提取-1,再根据分式的符号变化规律得出即可.
解答 解:-$\frac{1}{1-x}$=-$\frac{1}{-(x-1)}$=$\frac{1}{x-1}$,
故选D.
点评 本题考查了分式的基本性质的应用,能正确根据分式的基本性质进行变形是解此题的关键,注意:分式本身的符号,分子的符号,分母的符号,变换其中的两个,分式的值不变.

练习册系列答案
相关题目
4.菱形具有而平行四边形不一定具有的性质是( )
| A. | 两组对边分别平行 | B. | 两组对角分别相等 | ||
| C. | 对角线互相平分 | D. | 对角线互相垂直 |
1.计算3$\sqrt{2}$-$\sqrt{2}$的值是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
4.下列美丽的图案,其中是中心对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.已知9m=$\frac{2}{3}$,3n=$\frac{1}{2}$;则下列结论正确的是( )
| A. | 2m-n=$\frac{4}{3}$ | B. | 2m+n=-1 | C. | 2m-n=3 | D. | $\frac{2m}{n}$=3 |
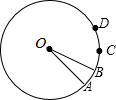 如图,圆心角∠AOB=20°,将$\widehat{AB}$旋转n°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20度.
如图,圆心角∠AOB=20°,将$\widehat{AB}$旋转n°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20度.