题目内容
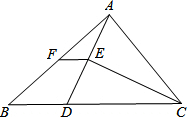 如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD与E,点F是AB的中点.若△ABD的周长是20,则△AFE的周长为( )
如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD与E,点F是AB的中点.若△ABD的周长是20,则△AFE的周长为( )| A、5 | B、10 | C、12 | D、15 |
考点:三角形中位线定理
专题:
分析:根据等腰三角形三线合一的性质可得AE=DE,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=
BD,然后判断出△AFE的周长=
△ABD的周长.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵DC=AC,CE是∠ACB的平分线,
∴AE=DE,
又∵点F是AB的中点,
∴EF是△ABD的中位线,
∴EF=
BD,
∴△AFE的周长=
△ABD的周长,
∵△ABD的周长是20,
∴△AFE的周长=10.
故选B.
∴AE=DE,
又∵点F是AB的中点,
∴EF是△ABD的中位线,
∴EF=
| 1 |
| 2 |
∴△AFE的周长=
| 1 |
| 2 |
∵△ABD的周长是20,
∴△AFE的周长=10.
故选B.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形三线合一的性质,熟记性质与定理是解题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,点P(3,4)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图所示,在一块平地上,李大爷家屋前14米远处有一颗大树,在一次强风中,这颗大树从离地面5米处折断倒下,量得倒下部分的长是13米.出门在外的李大爷担心自己的房子被倒下的树砸到,大树倒下时会砸到李大爷的房子吗?( )
如图所示,在一块平地上,李大爷家屋前14米远处有一颗大树,在一次强风中,这颗大树从离地面5米处折断倒下,量得倒下部分的长是13米.出门在外的李大爷担心自己的房子被倒下的树砸到,大树倒下时会砸到李大爷的房子吗?( )| A、一定不会 | B、可能会 |
| C、一定会 | D、以上答案都不对 |
用科学记数法表示5320000,正确的是( )
| A、5.32×106 |
| B、5.32×105 |
| C、532×104 |
| D、0.532×107 |
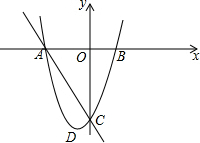 如图,抛物线y=
如图,抛物线y=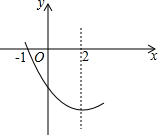 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论: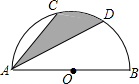 如图,点C,D是以2为直径的半圆上的两个点,CD∥AB,若∠CAD=25°,求图中阴影部分的面积.
如图,点C,D是以2为直径的半圆上的两个点,CD∥AB,若∠CAD=25°,求图中阴影部分的面积.