题目内容
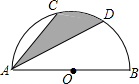如图，点C，D是以2为直径的半圆上的两个点，CD∥AB，若∠CAD=25°，求图中阴影部分的面积．考点：扇形面积的计算
专题：
分析：连接OC，OD，判断出阴影部分的面积=扇形OCD的面积，根据扇形的面积公式即可求解．
解答：解：连接OC，OD，
∵∠CAD=25°，
∴∠COD=50°，
∵AB∥CD，
∴△ACD的面积=△COD的面积，
∴阴影部分的面积=弓形CD的面积+△COD的面积=扇形OCD的面积=
=
π，
即阴影部分的面积是
π．
∵∠CAD=25°，
∴∠COD=50°，
∵AB∥CD，
∴△ACD的面积=△COD的面积，
∴阴影部分的面积=弓形CD的面积+△COD的面积=扇形OCD的面积=
| 50π×12 |
| 360 |
| 5 |
| 36 |
即阴影部分的面积是
| 5 |
| 36 |
点评：本题考查了扇形的面积公式的应用，理解阴影部分的面积=扇形COD的面积是解此题的关键．
练习册系列答案
相关题目
把2x2-4x分解因式，结果正确的是（ ）
| A、（x+2）（x-2） |
| B、2x（x-2） |
| C、2（x2-2x） |
| D、x（2x-4） |
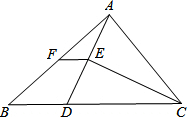如图，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CE交AD与E，点F是AB的中点．若△ABD的周长是20，则△AFE的周长为（ ）
如图，⊙O上有A，B，C，D四点，其中∠A=80°，那么∠C的度数是（ ）| A、40° | B、60° |
| C、80° | D、100° |
如图，在Rt△ABC中，斜边AB的中垂线DE交BC于D，连接AD，若∠1：2=2：5，求∠B、∠BAC的度数．
如图，在标号的11个角中同位角有
如图，已知∠AOB和点P．