题目内容
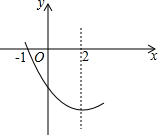 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;
②4a-2b+c<0;
③4a+b=0;
④抛物线与x轴的另一个交点是(5,0);
⑤点(-3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是
考点:二次函数图象与系数的关系
专题:
分析:根据抛物线的图象,数形结合,逐一解析判断,即可解决问题.
解答: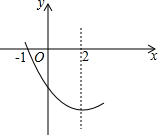 解:∵抛物线的对称轴为x=2,
解:∵抛物线的对称轴为x=2,
∴-
=2,b=-4a,4a+b=0,故③正确;
∵抛物线开口向上,
∴a>0,b<0;由图象知c<0,
∴abc>0,故①正确;
由抛物线的单调性知:当x=-2时,y>0,
即4a-2b+c>0,故②错误;
∵
=2,而对称轴方程为 x=2,
∴抛物线与x轴的另一个交点是(5,0),故④正确.
∵当
=2时,m=7,而6<7,
∴点(6,y2)在点(7,y3)的下方,
由抛物线的对称性及单调性知:y1<y2,故⑤错误;
故答案为:①③④.
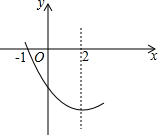 解:∵抛物线的对称轴为x=2,
解:∵抛物线的对称轴为x=2,∴-
| b |
| 2a |
∵抛物线开口向上,
∴a>0,b<0;由图象知c<0,
∴abc>0,故①正确;
由抛物线的单调性知:当x=-2时,y>0,
即4a-2b+c>0,故②错误;
∵
| -1+5 |
| 2 |
∴抛物线与x轴的另一个交点是(5,0),故④正确.
∵当
| -3+m |
| 2 |
∴点(6,y2)在点(7,y3)的下方,
由抛物线的对称性及单调性知:y1<y2,故⑤错误;
故答案为:①③④.
点评:该题主要考查了二次函数的图象与系数的关系、抛物线的单调性、对称性及其应用问题;灵活运用有关知识来分析、解答是关键.

练习册系列答案
相关题目
分式
,
,
,
中最简分式有( )
| a |
| x |
| x+y |
| x2-y2 |
| 2a-b |
| 4a2-4ab+b2 |
| x+y |
| x-y |
| A、1个 | B、2个 | C、3个 | D、4个 |
某产品原价100元,提价10%后又降价了10%,则现在的价格是( )
| A、90元 | B、110元 |
| C、100元 | D、99元 |
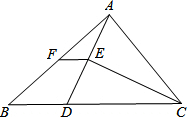 如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD与E,点F是AB的中点.若△ABD的周长是20,则△AFE的周长为( )
如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD与E,点F是AB的中点.若△ABD的周长是20,则△AFE的周长为( ) 如图,在Rt△ABC中,CD为斜边AB上的高,已知BC=4
如图,在Rt△ABC中,CD为斜边AB上的高,已知BC=4 如图,在Rt△ABC中,斜边AB的中垂线DE交BC于D,连接AD,若∠1:2=2:5,求∠B、∠BAC的度数.
如图,在Rt△ABC中,斜边AB的中垂线DE交BC于D,连接AD,若∠1:2=2:5,求∠B、∠BAC的度数.