题目内容
19.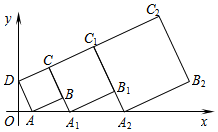 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为$\frac{64}{27}\sqrt{10}$.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为$\frac{64}{27}\sqrt{10}$.
分析 根据勾股定理求出AD,进而得到AB的长度,利用三角形相似的判定,证明△ABA1∽△DOA,得出BA1的长度,进而得到CA1的长度,同理可得第三个正方形,第四个正方形的边长.
解答 解:∵点A的坐标为(1,0),点D的坐标为(0,3),
∴OA=1,OD=3,
∵∠AOD=90°,
∴AD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,AB=AD=$\sqrt{10}$,
∴∠ODA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴$\frac{B{A}_{1}}{OA}=\frac{AB}{OD}$,即$\frac{B{A}_{1}}{1}=\frac{\sqrt{10}}{3}$,解得:BA1=$\frac{\sqrt{10}}{3}$,
∴CA1=$\frac{4\sqrt{10}}{3}$,
同理,可得:C1A2=$(\frac{4}{3})^{2}\sqrt{10}$,
∴第4个正方形的边长为$(\frac{4}{3})^{3}\sqrt{10}$=$\frac{64}{27}\sqrt{10}$,
故答案为:$\frac{64}{27}\sqrt{10}$.
点评 本题主要考查了点的规律,综合运用了正方形的性质、勾股定理、相似三角形的性质和判定等知识,能熟练运用三角形的性质和判定求出相关线段的长度是解决此题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
14.我校为了解七年级男同学参加课外体育运动的情况,随机调查了50名七年级男同学,其中,参加篮球运动的有14人,乒乓球运动的有11人,足球运动的有13人,其余参加羽毛球运动.则参加羽毛球运动的频率是( )
| A. | 0.28 | B. | 0.28 | C. | 0.26 | D. | 0.24 |
11.某商品的进价为每件20元.当售价为每件30元时,每天可卖出100件,现需降价处理,且经市场调查:每降价1元,每天可多卖出10件.现在要使每天利润为750元,每件商品应降价( )元.
| A. | 2 | B. | 2.5 | C. | 3 | D. | 5 |
8.一组数据2,5,6,x,4的平均数是4,这组数据的方差是( )
| A. | 10 | B. | 2 | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
9.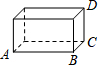 如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
 如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )| A. | 3$\sqrt{5}$ | B. | $\sqrt{41}$ | C. | $\sqrt{29}$ | D. | 5 |