题目内容
9.已知AB是⊙O的直径,弦CD⊥AB,E为垂足,CD=8,OE=1,则AB=2$\sqrt{17}$.分析 根据垂径定理和勾股定理可以求得半径的长,从而可以求得AB的长.
解答 解:∵AB是⊙O的直径,弦CD⊥AB,E为垂足,CD=8,OE=1,
∴CE=4,
∴OC=$\sqrt{O{E}^{2}+C{E}^{2}}=\sqrt{{1}^{2}+{4}^{2}}=\sqrt{17}$,
∴AB=2OC=2$\sqrt{17}$,
故答案为:2$\sqrt{17}$.
点评 本题考查垂径定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用垂径定理和勾股定理解答.

练习册系列答案
相关题目
19.某电动自行车厂三月份的产量为1000辆,由于市场需求量不断增大,五月份的产量提高到l210辆,剩该厂四、五月份的月平均增长率为( )
| A. | 12.1% | B. | 20% | C. | 21% | D. | 10% |
1.在一个不透明的布袋中装有3个白球和1个红球,它们除颜色不同外,其余均相同.从中随机一次摸出两个球,则两个球都是白球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.
如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.

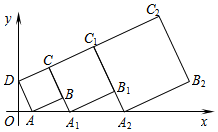 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为$\frac{64}{27}\sqrt{10}$.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为$\frac{64}{27}\sqrt{10}$.