题目内容
19.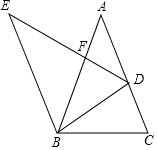 如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
分析 先利用旋转的性质得BC=BD,∠C=∠EDB,∠A=∠E,∠CBD=∠ABE,再利用等腰三角形的性质和三角形内角和证明∠ABD=∠A,则BD=AD,然后证明△BDC∽△ABC,则利用相似比得到BC:AB=CD:BC,即BF:(AF+BF)=AF:BF,最后利用解方程求出AF与BF的比值.
解答 解:∵△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,
∴BC=BD,∠C=∠EDB,∠A=∠E,∠CBD=∠ABE,
∵∠ABE=∠ADF,
∴∠CBD=∠ADF,
∵DB=BF,
∴BF=BD=BC,
而∠C=∠EDB,
∴∠CBD=∠ABD,
∴∠ABC=∠C=2∠ABD,
∵∠BDC=∠A+∠ABD,
∴∠ABD=∠A,
∴BD=AD,
∴CD=AF,
∵AB=AC,
∴∠ABC=∠C=∠BDC,
∴△BDC∽△ABC,
∴BC:AB=CD:BC,即BF:(AF+BF)=AF:BF,
整理得AF2+BF•AF-BF2=0,
∴AF=$\frac{-1+\sqrt{5}}{2}$BF,
即AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
故答案为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和相似三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC→CB运动,到点B停止.过点P作PD⊥AB于点D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动4秒时,PD的长是( )
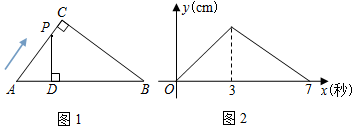

| A. | 2.4cm | B. | 1.5cm | C. | 1.8cm | D. | 1.2cm |
8.今年我市有近5000多名考生参加中考,为了解这些考生的数学成绩,从中抽取300名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这300名考生是总体的一个样本 | B. | 近5000多名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 300名考生是样本容量 |
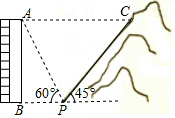 图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.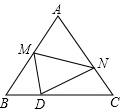 如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$.
如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$.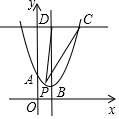 如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.
如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.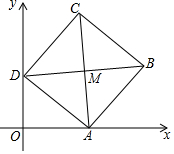 在平面直角坐标系中,正方形ABCD的顶点A,D分别在x轴、y轴正半轴上,AC,BD交于点M,若OA=8,OD=6,则点M的坐标为(7,7).
在平面直角坐标系中,正方形ABCD的顶点A,D分别在x轴、y轴正半轴上,AC,BD交于点M,若OA=8,OD=6,则点M的坐标为(7,7).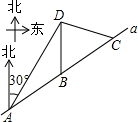 如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.
如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.