题目内容
 在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD做为直径作⊙O交AC于点E,连接DE并延长交BC的延长线于点F,且BD=BF.
在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD做为直径作⊙O交AC于点E,连接DE并延长交BC的延长线于点F,且BD=BF.(1)求证:AC与⊙O相切;
(2)若BC=6,AD=4,求⊙O的面积.
考点:切线的判定
专题:
分析:(1)连接OE,求出OE∥BF推出∠AEO=90°,根据切线的判定推出即可;
(2)证△AOE=△ABC,得出关于r的方程,求出方程的解即可.
(2)证△AOE=△ABC,得出关于r的方程,求出方程的解即可.
解答:证明(1)连接OE,
∵OD=OE,
∴∠ODE=∠OED,
∵BD=BF,
∴∠IDF=∠F,
∴∠OED=∠F,
∴OE∥BF,
∴∠AEO=∠ACB=90°,
∴AC与⊙O相切;
(2)解:∵由(1)可知,∠AEO=∠ACB,又∠A=∠A,
∴△AOE=△ABC,
∴
=
,
设⊙O的半径为r,则
=
,
解得r=4(负数舍去),
∴⊙O的面积为π×42=16π.

∵OD=OE,
∴∠ODE=∠OED,
∵BD=BF,
∴∠IDF=∠F,
∴∠OED=∠F,
∴OE∥BF,
∴∠AEO=∠ACB=90°,
∴AC与⊙O相切;
(2)解:∵由(1)可知,∠AEO=∠ACB,又∠A=∠A,
∴△AOE=△ABC,
∴
| OE |
| BC |
| AO |
| AB |
设⊙O的半径为r,则
| r |
| 6 |
| r+4 |
| 2r+4 |
解得r=4(负数舍去),
∴⊙O的面积为π×42=16π.
点评:本题考查了切线的判定,等腰三角形的性质,平行线的性质和判定,相似三角形的性质和判定的应用,解此题的关键是求出∠AEO=90°和得出关于r的方程,用了方程思想难度适中.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若xy>0,则二次根式x
化为最简二次根式正确的是( )
-
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|

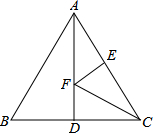 如图,等边△ABC的边长为2,AD是BC边上的中线,F是AD边上的动点,E是AC边上的中点,若∠ECF=30°时,EF+CF的值为( )
如图,等边△ABC的边长为2,AD是BC边上的中线,F是AD边上的动点,E是AC边上的中点,若∠ECF=30°时,EF+CF的值为( )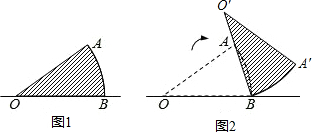 如图(1),扇形AOB中,OA=10,∠AOB=36°.若固定B点,将此扇形依顺时针方向旋转,得一新扇形A′O′B,其中O′点在直线BA上,如图(2)所示,则O点旋转至O′点所经过的轨迹长度(弧长)为
如图(1),扇形AOB中,OA=10,∠AOB=36°.若固定B点,将此扇形依顺时针方向旋转,得一新扇形A′O′B,其中O′点在直线BA上,如图(2)所示,则O点旋转至O′点所经过的轨迹长度(弧长)为