题目内容
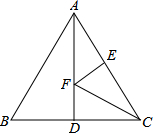 如图,等边△ABC的边长为2,AD是BC边上的中线,F是AD边上的动点,E是AC边上的中点,若∠ECF=30°时,EF+CF的值为( )
如图,等边△ABC的边长为2,AD是BC边上的中线,F是AD边上的动点,E是AC边上的中点,若∠ECF=30°时,EF+CF的值为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、1+
|
考点:等边三角形的性质
专题:
分析:先根据等边三角形的性质求出AD的长∠CAD的度数,再由E是AC边上的中点,∠ECF=30°得出CF是∠ACD的平分线,故EF⊥AC,故EF=DF,再根据∠EDF=∠CAD=30°得出AF=CF,故AD=EF+CF,由此可得出结论.
解答:解:∵等边△ABC的边长为2,AD是BC边上的中线,
∴AD=AB•sin60°=2×
=
,AD⊥BC,∠CAD=30°.
∵E是AC边上的中点,∠ECF=30°,
∴CF是∠ACD的平分线,
∴EF⊥AC,
∴EF=DF.
∵∠EDF=∠CAD=30°,
∴AF=CF,
∴AD=EF+CF=
.
故选C.
∴AD=AB•sin60°=2×
| ||
| 2 |
| 3 |
∵E是AC边上的中点,∠ECF=30°,
∴CF是∠ACD的平分线,
∴EF⊥AC,
∴EF=DF.
∵∠EDF=∠CAD=30°,
∴AF=CF,
∴AD=EF+CF=
| 3 |
故选C.
点评:本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若x>y,则下列式子错误的是( )
| A、x2-3>y2-3 | ||||
| B、3-2x<3-2y | ||||
| C、x+3>y+2 | ||||
D、
|
下列四个数中最大的一个数是( )
A、-
| ||
| B、|-4| | ||
| C、0 | ||
| D、-4 |
 正常人的体温一般在36.5℃左右,但一天中的不同时刻 不尽相同,下图反映了一天24小时内小明体温的变化情况.
正常人的体温一般在36.5℃左右,但一天中的不同时刻 不尽相同,下图反映了一天24小时内小明体温的变化情况. 在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD做为直径作⊙O交AC于点E,连接DE并延长交BC的延长线于点F,且BD=BF.
在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD做为直径作⊙O交AC于点E,连接DE并延长交BC的延长线于点F,且BD=BF. 如图,梯形ABCD中,AB∥CD,AD=BC,O为梯形ABCD外一点,OA、OB分别交线段DC于点F、E,且OA=OB.
如图,梯形ABCD中,AB∥CD,AD=BC,O为梯形ABCD外一点,OA、OB分别交线段DC于点F、E,且OA=OB.