题目内容
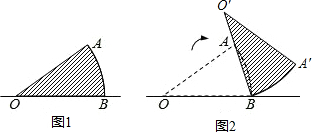如图（1），扇形AOB中，OA=10，∠AOB=36°．若固定B点，将此扇形依顺时针方向旋转，得一新扇形A′O′B，其中O′点在直线BA上，如图（2）所示，则O点旋转至O′点所经过的轨迹长度（弧长）为考点：弧长的计算,旋转的性质
专题：
分析：根据弧长公式，此题主要是得到∠OBO′的度数，再根据等腰三角形的性质即可求解．
解答：解：根据题意，知OA=OB．
又∵∠AOB=36°，
∴∠OBA=72°．
∴点旋转至O′点所经过的轨迹长度=
=4π．
故答案为4π．
又∵∠AOB=36°，
∴∠OBA=72°．
∴点旋转至O′点所经过的轨迹长度=
| 72π×10 |
| 180 |
故答案为4π．
点评：此题考查了旋转的性质，弧长公式，等腰三角形的性质，三角形内角和定理，求出∠OBO′的度数是解题的关键．
练习册系列答案
相关题目
在Rt△ABC中，∠ACB=90°，D是AB边上一点，以BD做为直径作⊙O交AC于点E，连接DE并延长交BC的延长线于点F，且BD=BF．若x＞y，则下列式子错误的是（ ）
| A、x2-3＞y2-3 | ||||
| B、3-2x＜3-2y | ||||
| C、x+3＞y+2 | ||||
D、
|
下列各式中，不能在实数范围内分解因式的是（ ）
| A、9x2+3xy2 | ||
| B、a2+2ab-b2 | ||
| C、-x2+25y2 | ||
D、x2-x+
|
下列方程是一元二次方程的是（ ）
| A、2x-y=1 | ||
| B、3x（x-1）=3x2+6 | ||
C、x+
| ||
| D、x2-3=0 |