题目内容
16．在△ABC中，E是AB上一点，D是AC上一点，AE=6，AC=15，AD=8，AB=20，求证：△AED∽△ACB．分析 首先根据已知得出AE：AC=AD：AB，又因为∠DAE=∠CAB，进而得出：△AED∽△ACB．
解答 
证明：∵AE=6，AC=15，AD=8，AB=20，
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{5}$，
又∵∠DAE=∠CAB，
∴△AED∽△ACB．
点评 此题主要考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解题关键．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
如图所示，要建造一面积为130平方米的仓库，仓库的一边靠墙（墙长16米），另三边用32米长的木板围成并在与墙平行的一边开一个1米宽的门，求仓库的长和宽各是多少？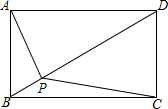
已知：如图，在矩形ABCD内有一点P．求证：PA2+PC2=PB2+PD2．