题目内容
13.化简或解方程、不等式组:(1)$\frac{1}{\sqrt{2}}$-$\sqrt{18}$+sin45°
(2)$\frac{\sqrt{3}tan30°}{2tan45°-1}$
(3)解方程:x2-4x+2=0;
(4)解不等式组:$\left\{\begin{array}{l}{\frac{x}{2}<\frac{x-1}{3}}\\{3(x+1)>4x+2}\end{array}\right.$.
分析 (1)先根据二次根式的性质,特殊角的三角函数值求出每一部分的值,再代入求出即可;
(2)先根据特殊角的三角函数值求出每一部分的值,再代入求出即可;
(3)先求出b2-4ac的值,再代入公式求出即可;
(4)先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:(1)原式=$\sqrt{2}$-3$\sqrt{2}$+$\frac{\sqrt{2}}{2}$
=-$\frac{3\sqrt{2}}{2}$;
(2)原式=$\frac{\sqrt{3}×\frac{\sqrt{3}}{3}}{2×1-1}$=1;
(3)x2-4x+2=0,
b2-4ac=(-4)2-4×1×2=8,
x=$\frac{4±\sqrt{8}}{2}$,
x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$;
(4)$\left\{\begin{array}{l}{\frac{x}{2}<\frac{x-1}{3}①}\\{3(x+1)>4x+2②}\end{array}\right.$
∵解不等式①得:x<-2,
解不等式②得:x<1,
∴不等式组的解集为:x<-2.
点评 本题考查了解一元一次不等式(组),二次根式的性质,特殊角的三角函数值,解一元二次方程的应用,能熟记知识点是解此题的关键.

练习册系列答案
相关题目
4.若点(3、4)在反比例函数y=$\frac{k}{x}$ (k≠0)的图象上,则该函数图象一定经过( )
| A. | (2、6) | B. | (2、-6) | C. | (4、-3) | D. | (3、-4) |
1.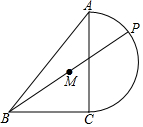 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )| A. | 2$\sqrt{2}$π | B. | $\sqrt{2}$π | C. | 2π | D. | 2$\sqrt{2}$ |
8.某化肥厂第一季度生产了m吨化肥,以后每季度比上一季度多生产x%,第三季度生产的化肥为n吨,则可列方程为( )
| A. | m(1+x)2=n | B. | m(1+x%)2=n | C. | (1+x%)2=n | D. | m+m (x%)2=n |
3.古代有这样一个寓言故事:驴子和骡子一同走,它们驮着不同袋数的货物,每袋货物都是一样重的.驴子抱怨负担太重,骡子说:“你抱怨干嘛,如果你给我一袋,那我所负担的就是你的两倍;如果我给你一袋,我们才恰好驮的一样多!”如果设驴子驮的袋数为x袋,骡子驮的袋数为y袋,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{\frac{y+1}{2}=(x-1)}\\{y+1=x-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y+1=\frac{1}{2}(x-1)}\\{y-1=x+1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y+1=2(x-1)}\\{y-1=x+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+1=2(x-1)}\\{y+1=x-1}\end{array}\right.$ |
