题目内容
5.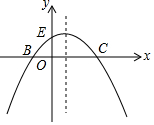 如图1,已知抛物线的方程C1:y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
如图1,已知抛物线的方程C1:y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.(1)若抛物线C1过点M(2,2),求实数m的值;
(2)在(1)的条件下,求△BCE的面积;
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
分析 (1)将x=2,y=2代入抛物线的解析式得到关于m的方程求得m的值即可;
(2)y=0可求得对应的x的值,则可得到B和点C的坐标,令x=0求得对应的y的值可求得点E的坐标,最后依据S△BCE=$\frac{1}{2}$BC•OE求解即可;
(3)连接EC交抛物线的对称轴于点H,连接BH,设对称轴与x轴的交点为P.先求得抛物线的对称轴为x=1,则点P(1,0),然后证明△PHC∽△OEC,依据相似三角形的性质可求得PH的长,则可得到点H的坐标;
(4)①过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.依据相似三角形的判定定理可知当BC2=CE•BF时,△BCE∽△FBC,设点F的坐标为(x,-$\frac{1}{m}$(x+2)(x-m)),由$\frac{FF'}{BF'}=\frac{EO}{CO}$列出关于x的方程可求得x=m+2,从而得到点F′的坐标,依据锐角三角函数的定义可知:$\frac{CO}{CE}=\frac{BF'}{BF}$,从而可求得BF的长,最后依据列出关于m的方程求解即可;②作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,依据相似三角形的判定定理可知当BC2=BE•BF时,△BCE∽△BFC,由FF′=BF′,可求得F′(2m,0),然后可求得BF=2$\sqrt{2}$m+2$\sqrt{2}$,最后由BC2=BE•BF列出关于m的方程求解即可.
解答 解:(1)将x=2,y=2代入抛物线的解析式得:-$\frac{1}{m}$×4×(2-m)=2,
解得:m=4,
经检验:m=4是分式方程的解.
∴m的值为4.
(2)y=0得:0=-$\frac{1}{m}$(x+2)(x-m),解得x=-2或x=m,
∴B(-2,0),C(m,0).
由(1)得:m=4,
∴C(4,0).
将x=0代入得:y=-$\frac{1}{m}$×2×(-m)=2,
∴E(0,2).
∴BC=6,OE=2.
∴S△BCE=$\frac{1}{2}$BC•OE=$\frac{1}{2}$×6×2=6.
(3)如图1所示:连接EC交抛物线的对称轴于点H,连接BH,设对称轴与x轴的交点为P.
∵x=-$\frac{b}{2a}$,
∴抛物线的对称轴是直线x=1.
∴CP=3.
∵点B与点C关于x=1对称,
∴BH=CH.
∴BH+EH=EH+HC.
∴当H落在线段EC上时,BH+EH的值最小.
∵HP∥OE,
∴△PHC∽△EOC.
∴$\frac{HP}{CP}=\frac{EO}{CO}$,即$\frac{HP}{3}=\frac{2}{4}$.解得HP=$\frac{3}{2}$.
∴点H的坐标为(1,$\frac{3}{2}$).
(4)①如图2,过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.
∵BF∥EC,
∴∠BCE=∠FBC.
∴当$\frac{CE}{CB}=\frac{BC}{BF}$,即BC2=CE•BF时,△BCE∽△FBC.
设点F的坐标为(x,-$\frac{1}{m}$(x+2)(x-m)),由$\frac{FF'}{BF'}=\frac{EO}{CO}$,得$\frac{{\frac{1}{m}(x+2)(x-m)}}{x+2}=\frac{2}{m}$.
解得x=m+2.
∴F′(m+2,0).
∵∠BCE=∠FBC.
∴$\frac{CO}{CE}=\frac{BF'}{BF}$,得$\frac{m}{{\sqrt{{m^2}+4}}}=\frac{m+4}{BF}$,解得:$BF=\frac{{(m+4)\sqrt{{m^2}+4}}}{m}$.
又∵BC2=CE•BF,
∴${(m+2)^2}=\sqrt{{m^2}+4}×\frac{{(m+4)\sqrt{{m^2}+4}}}{m}$,整理得:0=16.此方程无解.
②如图3,作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,
∵OE=OB,∠EOB=90°,
∴∠EBO=45°.
∵∵∠CBF=45°,
∴∠EBC=∠CBF,
∴当$\frac{BE}{BC}=\frac{BC}{BF}$,即BC2=BE•BF时,△BCE∽△BFC.
在Rt△BFF′中,由FF′=BF′,得$\frac{1}{m}$(x+2)(x-m)=x+2,解得x=2m.
∴F′(2m,0).
∴BF′=2m+2,
∴BF=2$\sqrt{2}$m+2$\sqrt{2}$.
由BC2=BE•BF,得(m+2)2=2$\sqrt{2}$×(2$\sqrt{2}$m+2$\sqrt{2}$).解得$m=2±2\sqrt{2}$.
∵m>0,
∴m=2+2$\sqrt{2}$.
综上所述,点m的值为2+2$\sqrt{2}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的性质、轴对称图象的性质,两点之间线段最短以及相似三角形的性质和判定,求出点F′的坐标,从而得到相关线段的长度是解题的关键.

 如图,函数y=kx与y=$\frac{m}{x}$的图象在第一象限内交于点A,过点A作AD垂直x轴于点D,且S△AOD=$\frac{3}{2}$.
如图,函数y=kx与y=$\frac{m}{x}$的图象在第一象限内交于点A,过点A作AD垂直x轴于点D,且S△AOD=$\frac{3}{2}$.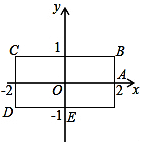 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是(-1,1).
如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是(-1,1).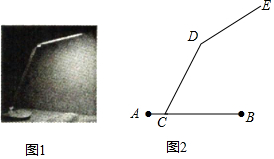 如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)
如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)