题目内容
20.如图①,A(8,6),AB⊥y轴于B点,点R从原点O出发,沿y轴正方向匀速运动,同时点Q从点A出发,沿线段AB向点B以相同的速度匀速运动,当点Q到达点B时,两点同时停止运动,设运动的时间为t秒.(1)点B的坐标为(0,6);
(2)过R点作RP⊥OA交x轴于点P,当点R在OB上运动时,△BRQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,如图②,求点R的运动速度;
(3)如果点R、Q保持(2)中的速度不变,在整个运动过程中,设△PRQ与△OAB的重叠部分的面积为y,请求出y关于t的函数关系式.

分析 (1)利用直线垂直于y轴,得到该直线上的点纵坐标相等即可;
(2)根据题意列出方程S=$\frac{1}{2}$(6-2x)(8-2x),求解即可;
(3)先求出点R的运动速度为2,确定出0≤t总≤4,再分两种情况计算用面积的和差即可.
解答 解:(1)A(8,6),AB⊥y轴于B点,
则B(0,6).
故答案为(0,6);
(2)设运动速度为x,
∵△BRQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分
∴S=$\frac{1}{2}$(6-2x)(8-2x),
∴$\frac{1}{2}$(6-2x)(8-2x)=4,
∴x1=2,x2=5(舍),
(3)如图①,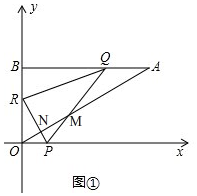 ∵PR⊥OA,
∵PR⊥OA,
∴∠ROA+∠ORP=90°.
∵∠ROA+∠BAO=90°,
∴∠ORP=∠BAO
∴tan∠BAO=$\frac{6}{8}$,tan∠ORP=$\frac{OP}{OR}$,
∴$\frac{OP}{2t}=\frac{6}{8}$,
∴OP=$\frac{3}{2}$t,
∵Q(8-2t,6),
∴$\frac{OP}{AQ}=\frac{3}{4}$,
∵△OPM∽△AQM,
∴△OPM的边OP与△AQM的边AQ上的高的比为$\frac{3}{4}$,
∴△AQM的边AQ上的高为$\frac{24}{7}$,
∴y=S△ABO-S△AQM-S△BRQ-S△ORN=$\frac{250-40\sqrt{30}}{175}$t2+t,
设点R的运动速度为x,当t=2时,$\frac{1}{2}$(8-2x)(6-2x)=4,
∴x1=2,x2=5(舍),
即:点R的运动速度为2,
∴0≤t总≤4,
①当0≤t≤3时,
y=S△AOB-S△BQR-S△AQN-S△RMO
=$\frac{1}{2}$×6×8-$\frac{1}{2}$(8-2t)(6-2t)-$\frac{1}{2}$×2t×$\frac{24}{7}$-×$\frac{1}{2}$×$\frac{6}{5}$t×$\frac{8}{5}$t
=-$\frac{74}{25}$t2+$\frac{74}{7}$t.
②当3<t≤$\frac{25}{7}$时,
y=$\frac{27}{50}$t2-$\frac{87}{7}$t+$\frac{75}{2}$
③当$\frac{25}{7}$<t≤4时,
y=-$\frac{27}{50}$t2+$\frac{87}{7}$t-$\frac{75}{2}$
点评 此题是二次函数综合题,主要考查了运动中线段的表示,几何图形的面积的计算,解本题的关键是用时间表示出线段,难点是计算量太大.

 名校课堂系列答案
名校课堂系列答案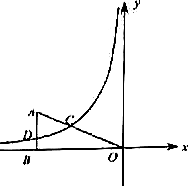 已知:在平面直角坐标系xOy中,过点A(-5,2)向x轴作垂线,垂足为B,连接AO,点C在线段AO上,且AC:CO=2:3,反比例函数y=$\frac{k}{x}$的图象经过点C,与边AB交于点D.
已知:在平面直角坐标系xOy中,过点A(-5,2)向x轴作垂线,垂足为B,连接AO,点C在线段AO上,且AC:CO=2:3,反比例函数y=$\frac{k}{x}$的图象经过点C,与边AB交于点D.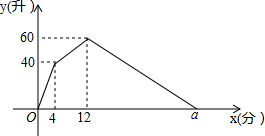 某容器装有两个相同的注水管和一个出水管,注水管的注水速度和出水管的出水速度均为定值,从某一时刻开始,打开两个注水管向容器内注水4分钟,然后关闭一个注水管,打开出水管.出水管出水8分钟,关闭另一个注水管,容器内的水放完时关闭出水管.容器内的水量y(升)与时间x(分)之间的函数图象如图所示.
某容器装有两个相同的注水管和一个出水管,注水管的注水速度和出水管的出水速度均为定值,从某一时刻开始,打开两个注水管向容器内注水4分钟,然后关闭一个注水管,打开出水管.出水管出水8分钟,关闭另一个注水管,容器内的水放完时关闭出水管.容器内的水量y(升)与时间x(分)之间的函数图象如图所示.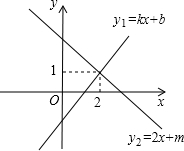 直线y1=kx+b和y2=2x+m相交于点A(2,1).
直线y1=kx+b和y2=2x+m相交于点A(2,1).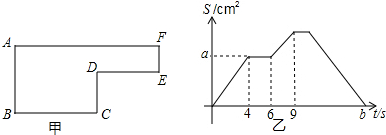
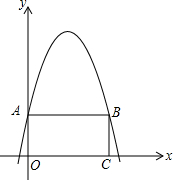 如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.
如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.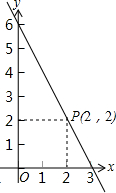 函数y=-2x+6的图象如图所示,P(2,2)是图象上的一点,观察图象回答问题.
函数y=-2x+6的图象如图所示,P(2,2)是图象上的一点,观察图象回答问题.