题目内容
6.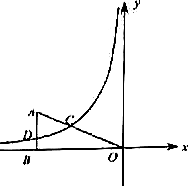 已知:在平面直角坐标系xOy中,过点A(-5,2)向x轴作垂线,垂足为B,连接AO,点C在线段AO上,且AC:CO=2:3,反比例函数y=$\frac{k}{x}$的图象经过点C,与边AB交于点D.
已知:在平面直角坐标系xOy中,过点A(-5,2)向x轴作垂线,垂足为B,连接AO,点C在线段AO上,且AC:CO=2:3,反比例函数y=$\frac{k}{x}$的图象经过点C,与边AB交于点D.(1)求反比例函数的解析式;
(2)求△BOD的面积.
分析 (1)由A点的坐标结合中点的坐标公式可得出点C的坐标,将点C的坐标代入到反比例函数解析式即可求出k值,从而得出反比例函数的解析式;
(2)AB⊥x轴于B,于是得到OB=5,根据三角形的面积公式即可得到结论.
解答 解:(1)∵AC:CO=2:3,点A(-5,2),
∴C点的坐标为(-3,$\frac{6}{5}$),
将点C(-3,$\frac{6}{5}$),代入到反比例函数y=$\frac{k}{x}$中得:
$\frac{6}{5}$=$\frac{k}{-3}$,解得:k=-$\frac{18}{5}$.
∴反比例函数的解析式为y=-$\frac{18}{5x}$;
(2)∵AB⊥x轴于B,
∴OB=5,
把x=-5代入y=-$\frac{18}{5x}$得y=$\frac{18}{25}$,
∴△BOD的面积=$\frac{1}{2}$×5×$\frac{18}{25}$=$\frac{9}{5}$.
点评 本题考查了待定系数法求函数解析式以及三角形的面积公式,解题的关键是求出点C的坐标.

练习册系列答案
相关题目
11.若关于x的二次三项式x2-ax+36是一个完全平方式,那么a的值是( )
| A. | 12 | B. | ±12 | C. | 6 | D. | ±6 |
 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD,若∠A=25°,请你求出∠C的度数.
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD,若∠A=25°,请你求出∠C的度数.
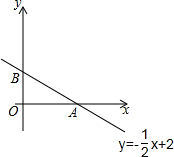 在平面直角坐标系中,已知直线l:y=-$\frac{1}{2}$x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
在平面直角坐标系中,已知直线l:y=-$\frac{1}{2}$x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.