题目内容
10.在矩形纸片ABCD中,AB=6,BC=8.(1)如图①,将矩形纸片沿AN折叠,点B落在对角线AC上的点E处,求BN的长;
(2)如图②,点M为AB上一点,将△BCM沿CM翻折至△ECM,ME与AD相交于点G,CE与AD相交于点F,且AG=GE,求BM的长;
(3)如图③,将矩形纸片ABCD折叠,使顶点B落在AD边上的点E处,折痕所在直线同时经过AB、BC(包括端点),设DE=x,请直接写出x的取值范围:2≤x≤2$\sqrt{7}$.

分析 (1)设BN=x,在Rt△ENC中,由勾股定理得出方程,解方程即可;
(2)由ASA证明△GAM≌△GEF(ASA),得出GM=GF,AF=ME=BM=x,EF=AM=6-x,因此DF=8-x,CF=x+2,在Rt△DFC中,由勾股定理得出方程,解方程即可;
(3)当折痕所在直线经过点A时,如图1所示;此时DE最小=AD-AB=8-6=2;当折痕所在直线经过点C时,如图2所示:此时DE最大,CE=CB=8,由勾股定理得:DE=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$;∴x的取值范围是2≤x≤2$\sqrt{7}$;故答案为:2≤x≤2$\sqrt{7}$.
解答 解:(1)设BN=x,在Rt△ENC中,由勾股定理得:x2+42=(8-x),
解得:x=3,
∴BN=3;
(2)设BM=x,
由折叠的性质得:∠E=∠B=90°=∠A,
在△GAM和△GEF中,$\left\{\begin{array}{l}{∠A=∠E}&{\;}\\{AG=GE}&{\;}\\{∠AGM=∠EGF}&{\;}\end{array}\right.$,
∴△GAM≌△GEF(ASA),
∴GM=GF,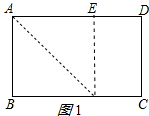
∴AF=ME=BM=x,EF=AM=6-x,
∴DF=8-x,CF=8-(6-x)=x+2,
在Rt△DFC中,由勾股定理得:(x+2)2=(8-x)2+62,
解得:x=$\frac{24}{5}$,
∴BM=$\frac{24}{5}$;
(3)当折痕所在直线经过点A时,如图1所示: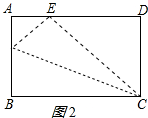
此时DE最小=AD-AB=8-6=2;
当折痕所在直线经过点C时,如图2所示:
此时DE最大,CE=CB=8,
由勾股定理得:DE=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$;
∴x的取值范围是2≤x≤2$\sqrt{7}$;
故答案为:2≤x≤2$\sqrt{7}$.
点评 本题是三角形综合题目,考查了矩形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握矩形的性质和全等三角形的判定与性质,由勾股定理得出方程是解决问题的关键.

 如图,垂直平分AB,交AC于点D,交AB于点E,连接BD,若AC=6cm,BC=4cm,则△BCD的周长为( )
如图,垂直平分AB,交AC于点D,交AB于点E,连接BD,若AC=6cm,BC=4cm,则△BCD的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
| A. | 20道 | B. | 21道 | C. | 22道 | D. | 23道 |
 探索与发现
探索与发现 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船,此时,遇险船在救生船的正东方向B处,现救生船沿着航线CB前往B处救援,求救生船到达B处行驶的距离?(参考数据:sin68°≈0.90,cos68°≈0.36,tan68°≈2.50,$\sqrt{3}$≈1.7)
如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船,此时,遇险船在救生船的正东方向B处,现救生船沿着航线CB前往B处救援,求救生船到达B处行驶的距离?(参考数据:sin68°≈0.90,cos68°≈0.36,tan68°≈2.50,$\sqrt{3}$≈1.7)