题目内容
15. 探索与发现
探索与发现(1)正方形ABCD中有菱形PEFG,当它们的对角线重合,且点P与点B重合时(如图1),通过观察或测量,猜想线段AE与CG的数量关系,并证明你的猜想;
(2)当(1)中的菱形PEFG沿着正方形ABCD的对角线平移到如图2的位置时,猜想线段AE与CG的数量关系,并证明你的猜想.
分析 (1)结论AE=CG.只要证明△ABE≌△CBG,即可解决问题.
(2)结论不变,AE=CG.如图2中,连接BG、BE.先证明△BPE≌△BPG,再证明△ABE≌△CBG即可.
解答 解:(1)结论:AE=CG.
理由:如图1中,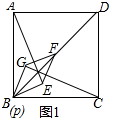
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD,
∵四边形PEFG是菱形,
∴BE=BG,∠EBD=∠GBD,
∴∠ABE=∠CBG,
在△ABE和△CBG中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBG}\\{BE=BG}\end{array}\right.$,
∴△ABE≌△CBG,
∴AE=CG.
(2)结论不变,AE=CG.
理由:如图2中,连接BG、BE.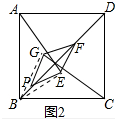
∵四边形PEFG是菱形,
∴PE=PG,∠FPE=∠FPG,
∴∠BPE=∠BPG,
在△BPE和△BPG中,
$\left\{\begin{array}{l}{PB=PB}\\{∠BPE=∠BPG}\\{PE=PG}\end{array}\right.$,
∴△BPE≌△BPG,
∴BE=BG,∠PBE=∠PBG,
∵∠ABD=∠CBD,
∴∠ABE=∠CBG,
在△ABE和△CBG中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBG}\\{BE=BG}\end{array}\right.$,
∴△ABE≌△CBG,
∴AE=CG.
点评 本题考查正方形的性质、菱形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.3的平方根是( )
| A. | 9 | B. | ±9 | C. | $\sqrt{3}$ | D. | $±\sqrt{3}$ |

 如图,在△ABC中,∠B与∠ACB互余,∠B=50°,∠3=20°,∠2是∠1的两倍,求证:DE∥BC.
如图,在△ABC中,∠B与∠ACB互余,∠B=50°,∠3=20°,∠2是∠1的两倍,求证:DE∥BC.
