题目内容
15.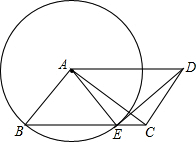 在平行四边形ABCD中,以点A为圆心,AB为半径的圆,交BC于点E.
在平行四边形ABCD中,以点A为圆心,AB为半径的圆,交BC于点E.(1)求证:△ABC≌△EAD;
(2)如果AB⊥AC,AB=6,AC=8,求EC的长.
分析 (1)直接利用平行四边形的性质得出BC=AD,AB=AE,AD∥BC,进而利用全等三角形的判定方法得出答案;
(2)利用勾股定理得出BC的长,再利用三角形面积求出BM的长,进而得出BE的长即可得出答案.
解答 (1)证明:∵在平行四边形ABCD中,以点A为圆心,AB为半径的圆,
∴BC=AD,AB=AE,AD∥BC,
∴∠B=∠AEB=∠DAE,
在△DAE和△CBA中,
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠DAE}\\{BC=AD}\end{array}\right.$,
∴△ABC≌△EAD;
(2)解:过点A作AM⊥BC于点M,
∵AB⊥AC,AB=6,AC=8,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=10,
∴AM×BC=AB×AC,
解得:AM=$\frac{24}{5}$,
故BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=$\frac{18}{5}$,
则BE=$\frac{36}{5}$,
故EC=10-$\frac{36}{5}$=$\frac{14}{5}$.
点评 此题主要考查了平行四边形的性质以及勾股定理和全等三角形的判定等知识,正确利用平行四边形的性质是解题关键.

练习册系列答案
相关题目
 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若∠1=70°,求∠2的度数.
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若∠1=70°,求∠2的度数.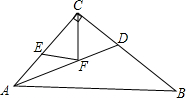 △ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.
△ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值. 某长方形广场除四角外都是空地,四角都是一块半径相同的四分之一圆的草坪,若圆形草坪的半径为r,长方形的长为a,宽为b,请用整式表示空地的面积,并指出这个整式是单项式还是多项式.若是单项式,指出它的系数;若是多项式,指出它有几项,各项的系数分别是多少?
某长方形广场除四角外都是空地,四角都是一块半径相同的四分之一圆的草坪,若圆形草坪的半径为r,长方形的长为a,宽为b,请用整式表示空地的面积,并指出这个整式是单项式还是多项式.若是单项式,指出它的系数;若是多项式,指出它有几项,各项的系数分别是多少? 我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题: